We begin with a sidebar for identifying whether a sequence of edge lengths admits a convex configuration:

Fact 1 : The edge lengths L₁ , L₂ , ..., L _n admit a convex configuration precisely if , for all i,
                                                                          


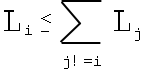
    Note that Fact 1 is always a useful piece of knowledge to have as support when one is delving into the world of convexity.


    Now, starting with a pair of distinct convex configurations C and C', we devise a way of reconfiguring C to reach C'. First, note that every vertex angle in C will either be equal to the corresponding vertex angle in C', or it will have to be increased or decreased by reconfigurations on the way from C to C'. So, labelling each angle of C +, -, or 0 depending on whether it has to increase, decrease or not change at all to match the corresponding angle in C', we have a labelling of vertices that can be used in conjuction with the following lemma:

Lemma 2 (Cauchy-Steinitz Lemma): In a +,-,0 labelling that comes from two distinct convex configurations, there are at least four sign alterations.

Proof: Each configuration is distinct and circular, and thus not all labels are zero, and the number of sign alterations must be even. This number also cannot be two, since then we have one chain of increasing angles, and one chain of decreasing angles, and this implies the lengthening of one chain and shortening of the other, which cannot be achieved.



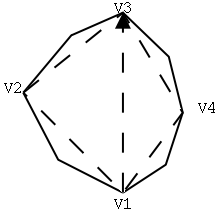
Taking four vertices V_i , V_j , V _k, V _l around the polygon with respective alternating signs of +,-,+,-, the quadrangle defined by the vertices can be flexed to achieve a label of 0 for one of the vertex angles-- this can be seen more clearly through the use of the lemma 3.

Lemma 3: Given a convex quadrangle V₁, V₂, V ₃, V₄, there is a motion that decreases the angles of V ₁ and V₃ , and increases the angles of V₂ and V ₄. The motion can continue until one of the angles reaches 0 or PI.

Proof: Consider a motion where V₁ is held fixed and V₃ moves along the directed line from V ₁ to V₃, and the distances between each vertex on the quadrangle and the vertices adjacent to it (V₁ and V₂ , V₂ and V₃, etc) remain constant. Then we can apply Euclid's Proposition I.25 to triangle V₁, V₂, V₃, and note that the angles at V₂ and V₄ must be increasing since |V₁ - V₃| is increasing. Since the angles are restricted to lie between 0 and PI, the convex quadrangle is maintained throughout the motion, and by Lemma 2 we have four sign alterations in the vertex angle labels, we see that the angles at V₁ and V₃ are decreasing throughout the motion.






Thus we can now define the main theorem for this part:

Theorem 1 : Given two convex configurations C and C' of the same sequence of edge lengths L1, ..., Ln, there is an angle-monotone motion from C to C' that involves O(n) moves each of which changes only four vertex angles at once.

Proof: By Lemma 2, we can find vertices Vi, Vj, Vk, V_l in cyclic order around the polygon in configuration C, and whose angles are labelled +, - , + , -, in that order. We obtain a convex quadrangle by specifying the rigidity of the subchains between each of the vertices, and apply motions to this quadrangle as per Lemma 3 until the label on one angle becomes 0. Repeating this process until all vertex angle labels are 0 yields a sequence of motions from C to C' with at most n moves, since each motion changes at least one non-zero label to zero, and each zero label remains unchanged during subsequent motions.


Proposition 1: Computing the motion in Theorem 1 can be done in O(n) time on a pointer machine with real numbers.

Proof: The first step in computing the motion in Theorem 1 is to maintain vertices V_i , V _j, V_k, V _l throughout the motion. In order to do this, we maintain four consecutive blocks I, J, K, L of the same sign--so I is a block of consecutive vertices labelled "+", J, is a block of consecutive vertices labelled "-", and so on. Each block can be created in linear time with an initial scan of the polygon's vertices in order, and each block contains pointers to its first and last vertices. The quadrangle vertices V _i , V_j , V _k , V_l are then identified as the first vertex in the corresponding block (so V_i is the first vertex in block I, V_j is the first vertex in J, ...), and when a motion changes a vertex angle's label to 0, the pointer for that vertex moves to the next one in the block. If block I becomes empty (i.e. the pointer for I is incremented after the last vertex in the block obtains a zero label), move block I to the set of "+"-labelled vertices after L, and if L becomes empty, move it to the block of -'s before I. If block K becomes empty, it advances to the block after L, J and L merge to form a new J block, and L advances to the block after the new K. Likewise, if J becomes empty, J moves to the block of -'s before I, blocks I and K merge to form a new K block, and I moves to the block of +'s before J (see below).







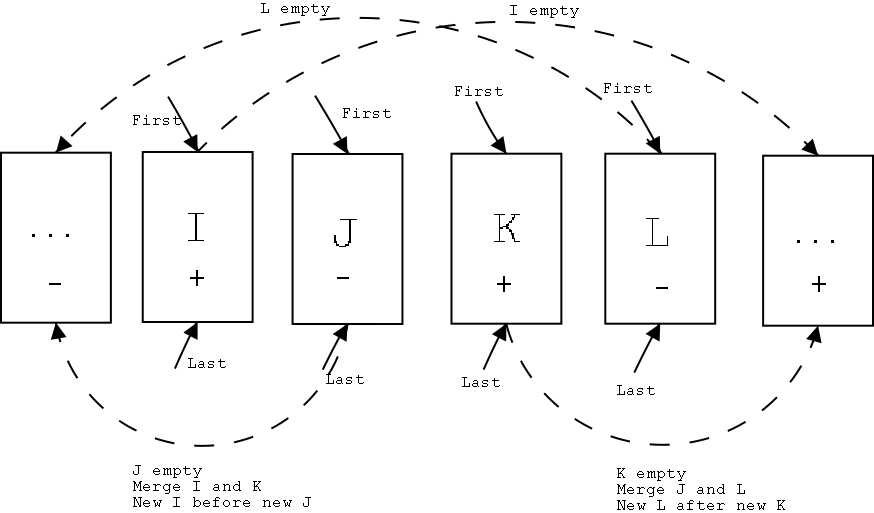
Now we apply the quadrangle motions of Lemma 3, including computing the finishing times for each of the vertex angles to reach a 0 label, and taking the vertex with the lowest of these computed times as the focal vertex in the Lemma. Since the algorithm effects a constant number of steps for each vertex in the polygon, and the number of iterations is a multiple of the number of vertices in the polygon, we have an O(n) algorithm for angle-monotone motions between two convex polygons with a common sequence of edge lengths.



Thus we see that a reconfiguration between any two convex polygons is indeed possible, and it can be computed in linear time with the most direct moves specified above.

---