The Simplical Depth Median (Liu 1988)
Another interpretation of the univariate median is that it is the point which lies inside the greatest number of intervals constructed from the data points. Liu generalized this idea as follows: Find the point in Rp which is contained in the most simplexes formed by subsets of p+1 data points (see fig.6). This median is affine equivariant. Not much information is available about the breakpoint.

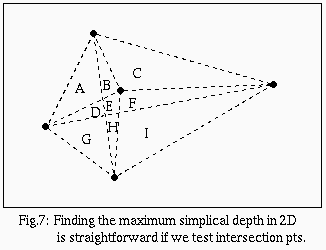
A brute force method of finding the simplical depth median in R2 is to partition the plane into cells which have segments between points as boundaries (fig.7 has cells A-I). First, notice that every point within a given cell has a "common destiny" (i.e. equal depth). Furthermore, a point on a boundary between two cells must have depth at least as much as any adjacent interior point. Similarly, an intersection point (where more than two cells meet) must have a depth at least as much as any adjacent boundary point. Therefore we must determine how many triangles contain each intersection point. There are O(n4) intersection points and O(n3) triangles for n points, so in O(n7) time, we can find the simplical depth median. Note that it is possible to find the simplical depth of a point in O(nlogn) time, so we can achieve a straightforward algorithm in O(n5logn).