
Convex Hull Stripping and Related Methods
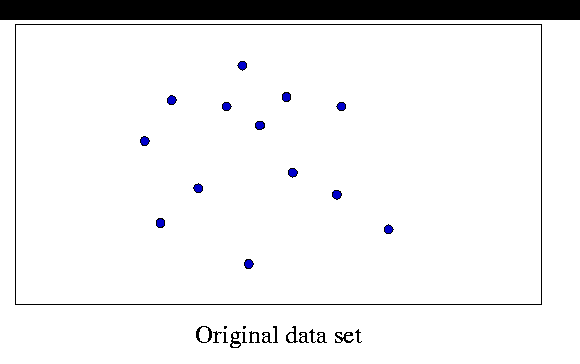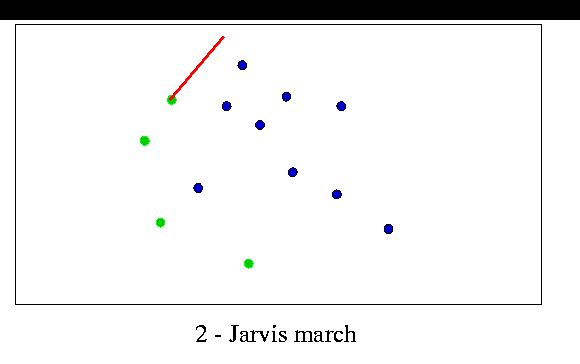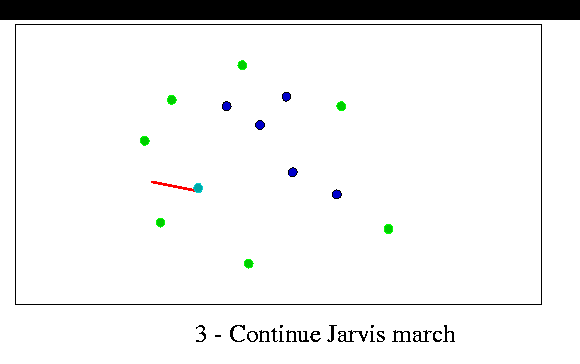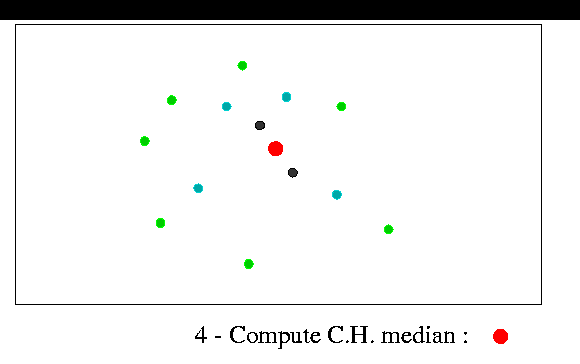
Perhaps the most intuitive visual interpretation of the univariate median is the idea of stripping away outlying data: we throw out the smallest and largest values recursively, until we are left with one or two. We can easily generalize this idea to higher dimensions. One way is to recursively strip away all points that are on the convex hull of the data set (fig.8). In the end, if we are not left with a unique point, we take the centroid. Other ways of removing outlying data exist, including minimum volume ellipsoid peeling. The two methods mentioned are affine equivariant, but may have very small breakdown points (fig.9).


Convex hull stripping by "brute force" should not take longer than O(n2logn) time. Finding the convex hull is Omega(nlogn), and in the worst case it is possible that only 3 data points will be removed each time, which leads to O(n) convex hull calculations.
The task can be done easily in O(n2) time by slightly modifying the Jarvis "gift-wrapping" convex hull algorithm. This algorithm takes O(hn) time, where h is the number of vertices on the hull. When modified to perform convex hull stripping, h adds up to n. An example is shown in the figure below.
Finally, convex hull peeling may be done in O(nlogn) time with a more complicated algorithm by Chazelle[3].