The Halfspace Median (Tukey 1975)

Note: Although Tukey is credited with the notion of the halfspace median, it was Hotelling in 1929 who introduced this interpretation for the univariate median.

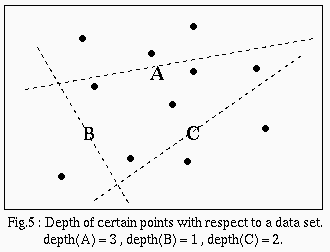
In order to define the halfspace median, we must first consider the notion of depth for a given point in R²: For each closed halfspace that contains the point, count the number of data points which are not in the halfspace. Take the minimum number found over all halfspaces to be the depth of that point. (ex: in 2D, for a given point, place a line through it so that the number of data on one side of the line is minimized).

The halfspace median of a data set is any point in R^p which has maximum depth.

The halfspace median is generally not a unique point. However the set of points of maximal depth is guaranteed to be a closed, bounded convex set. This median is affine equivariant, and can have a breakdown point between 1/(p+1) and 1/3.

Notice that any point outside of the convex hull of the data has depth zero. To find the region of maximum depth in R², we can use the fact that its boundaries are segments of lines passing through pairs of data. In other words, the vertices of the desired region must be intersection points of lines through pairs of data. There are O(n⁴) intersection points, and it takes O(nlogn) time to find the depth of one point, so in O(n⁵logn) time, we can find the intersection points of maximum depth. We may find the convex hull of these points in O(nlogn) time, and then compute the centroid if we do not have a unique point. Thus the overall time complexity is O(n⁵logn).

Note: The halfspace median may be found in O(n²log²n) time with a slightly more complicated method (Rousseeuw '98).

UPDATE