Mid-Point Smoothing Algorithm

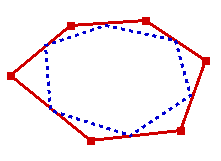
Definition:

The idea behind mid-point smoothing is very simple. Given an input polygon, we construct a mid-point smoothed version of the polygon by joining the mid-points of the edges of the polygon in the order in which they are encountered. The following figure shows an example of the application of this algorithm on an input polygon once.

A more mathematical definition of the algorithm follows:

Let P be a polygon given by

P={ (x₁,y₁), (x₂,y₂),...., (x_n,y_n) } where n is the number of vertices of the P.

The descendant M of P is defined as

M={ ((x₁+x₂)/2,(y₁+y₂)/2), ((x₂+x₃)/2,(y₂+y₃)/2), ..., ((x_n+x₁)/2,(y_n+y₁)/2) }

Properties:

Studying this algorithm in more detail, one comes up with various interesting observations about its behavior. In what follows, we group under the headings "Advantages" and "Disadvantages" the most important desirable and undesirable properties, respectively. We then list some other properties of the algorithm, some of which are pathological cases that may not arise in general.

Advantages:

Simple, but Effective
Fast
Complexity: O(kn) for k iterations

Disadvantages:

Same number of vertices

*This is considered undesirable because one of the requirements of preprocessing is usually also data reduction. This allows for faster classification and less demanding requirements on hardware (like memory or disk space).
Quickly erodes shape

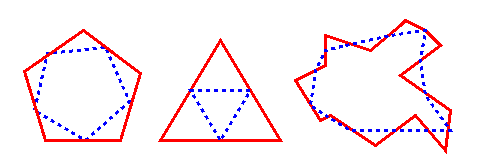
Most shapes result in convex polygons

A convex polygon is one such that if you choose any two points inside it, the line segment joining the two points lies inside the polygon. If the polygon is not convex, portions of the line segment would lie outside the polygon. For example, the polygon on the right below is not convex. Now, studying the mid-point smoothing algorithm, we observe that after a sufficient number of applications of such an algorithm, most shapes (convex or non-convex) eventually become convex.

May result in non-simple polygons

A non-simple polygon may be thought of as one that self intersects. As can be seen from the following figure, even though we start out with a simple polygon, just one application of the mid-point smoothing algorithm leaves us with a non-simple polygon. This may not always be desirable. However, successive applications of the algorithm give us simple polygons once again (albeit eroded ones).

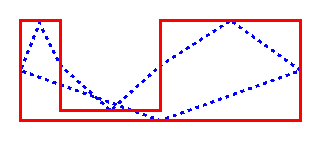
May result in oscillations

The polygons in the following figure show interesting examples. On the right, we start out with a non-simple polygon, and, no matter how many times we apply the algorithm, the output polygon maintains the shape of the input one. This is an example where a shape never becomes simple and eventually convex. On the left, we start out with a simple polygon. Applying the mid-point algorithm once, we obtain a non-simple polygon. Applying the algorithm once again, we find that the output polygon is a scaled replica of the input polygon. That is, if we scale this output in the x-direction, we'll find that it duplicates the input polygon. So, we effectively oscillate between a simple and a non-simple shape when we apply the algorithm successively. It is interesting to note that this behavior happens only for a specific ratio of dimensions (this ratio is the GOLDEN MEAN).