TAXICAB GEOMETRY???
In classical Euclidean geometry, the measure of the distance between two points, say A and B is calculated using the well known formula: d(A,B) = sqrt ((xA-xB)2 + (yA-yB)2 )
This is certainly the most intuitive notion of distance there is. However, it is not the only reasonable notion of distance. The theory of metric spaces is concerned with the differences and similarities of different definitions of distance. One interesting example of a redefinition of distance is the so-called 1st order Minkowski distance defining: d(A,B) = |xA-xB| + |yA-yB|
In simple terms, the distance is defined as the sum of the vertical and horizontal distance of the two points. We might notice that this definition of distance is fairly natural: it is the minimum distance that a taxicab would need to travel to reach point B from point A, if all streets are only oriented vertically and horizontally. For this reason, this metric is often referred to as the Manhattan metric.
Many geometric figures, like circles, ellipses, parabolas, are defined in terms of distance. For instance, a circle is just the set of points whose distance to the center is the radius. These of course start to look quite different if we use another measure of distance. The example of the circle is probably the most famous one.

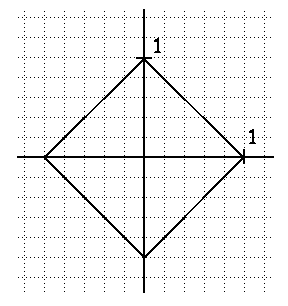
Taxicab circle
Note that we obtain a square if we use the taxicab metric. (Of course, this is not a solution to the famous problem of squaring the circle!) In general, conics (i.e. hyperbolas, parabolas, ellipses) will start looking "squarish" under the taxicab distance. Here are two examples, taken from the web page of Julie VanBelkum.
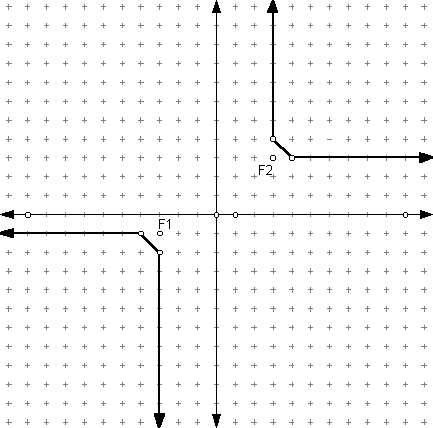
Taxicab Hyperbola
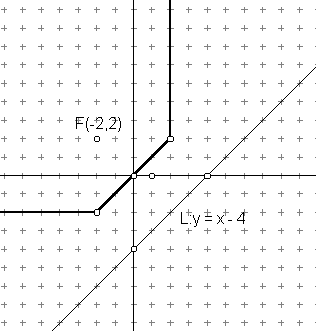
taxicab parabola
Another important geometric figure defined in terms of distance, is
the locus of points which are equidistant to two points A and B. In Euclidean
geometry, this is just the perpendicular bissector of the line segment
[AB]. The situation is not as simple in taxicab geometry. We need to consider
four basic examples:
|
|
|
|
Case 1: |xA-xB| < |yA-yB| |
Case 2: xA = xB |
|
|
|
|
Case 3: |xA-xB| > |yA-yB| |
Case 4: |xA-xB| = |yA-yB| |
These should be fairly easy to understand. Note that when xA =
xB, the euclidean and taxicab midsets coincide. In cases 1 and
3, t he midset consists only of vertical or horizontal segmentsoutside
of the rectangle defined by A and B and of a single line segment of slope
1 or -1 inside it. We also get a peculiar figure in the last case: all
the points in the lower-left and top-right corners are actually equidistant
to A and B in taxicab geometry!
| Back to the main page |