Hysteresis Smoothing for X-Monotonic Polygonal Chains

Usually in some applications, the system is driven by some external input which
could be an output of another system/process. In most cases this output contains
noise, and before it is applied, smoothing is performed on it to remove most of
the noise. The input considered in this report will be thought of as a single-
valued one dimensional function, g(x). The function g(x) can be thought of as
a polygonal chain in the x - y=g(x) plane (see figure 1).
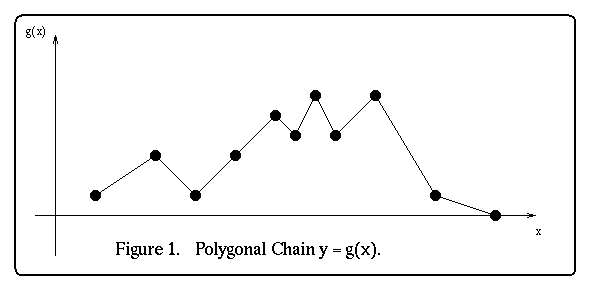
In this report we will look at one such method of smoothing called
hysteresis smoothing. Hysteresis smoothing is a method of smoothing
polygonal chains such that local minima/maxima within a certain threshold value
t is smoothed out (removed).
This is how it is done :
Let P = be a polygonal chain monotonic in the x direction.
Let t be the threshold value.
Form a chain U = <u1,...,un>, which is an exact copy of P but translated by t/2
in the positive y direction. Also let L = <l1,...,ln> be an exact copy of P but
translated by t/2 in the negative y direction. See figure 2 below.
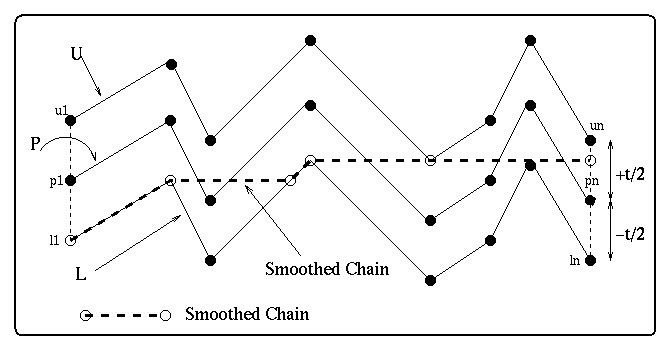 Lastly, connect u1 and l1 to p1, un and ln to pn, to form a monotonic polygon in
Lastly, connect u1 and l1 to p1, un and ln to pn, to form a monotonic polygon in
the x direction, B = <l1, p1, u1,...,un,pn,ln,...,l1>. The smoothed chain, S,
(see figure 2) is produced as follows: First we rotate the polygon B by 90 degrees
so that it becomes monotonic in the y direction. Now, imagine that l1 provides
a continuous supply of water and trace the path of the resulting waterfall
inside the polygon B (u1 could have done as well). The path of the waterfall is
the hysteresis-smoothed chain.
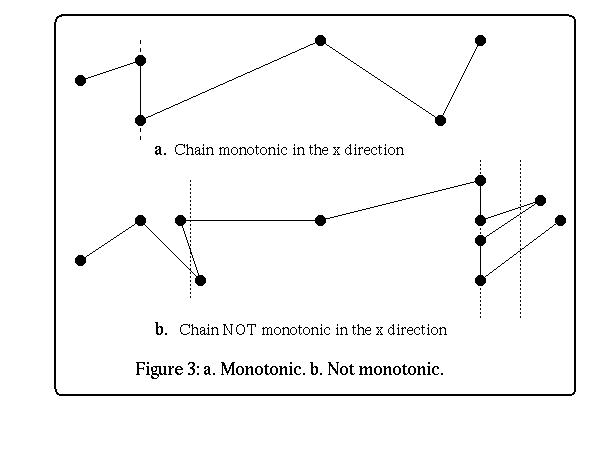
We will discuss only the algorithm for polygonal chains monotonic in the x
direction. A polygonal chain is monotonic in the x direction if every vertical
line intersecting it does so in at most one point or one line segment (see figure
3(a) and 3(b)). This implementation is for a polygon B monotonic in the
x direction (it was not rotated by 90 degrees!).
Notation
P = denotes the input polygonal chain with its vertices labeled
from left to right.
p(i).x or pi.x --- is the x coordinate of pi, and
p(i).y or pi.y --- is the y coordinate of pi.
t = threshold.
SEG(pi, pj) = Line segment between points pi and pj.
Algorithm
1. If p1.x <= p2.x <= ... <= pn.x is NOT satisfied the reject and stop.
P is not monotonic in the x direction.
2. Form the upper chain U = <(p1.x,p1.y + t/2),...,(pn.x,pn.y + t/2)> and
the lower chain L = <(p1.x,p1.y + t/2),...,(pn.x,pn.y + t/2)>.
3. STACK Q <-- empty;
POINT T, V, Last;
T <-- l1;
PUSH(Q,l1);
WhichChain <-- L;
Last.x <-- ln.x;
Last.y <-- l1.y;
T_changes <-- FALSE;
For> i := 2 to n-1 Do
BEGIN (* for *)
3.1 If li.y = T.y
{
PUSH(Q,li);
WhichChain <-- L;
T_changes <-- TRUE;
}
3.2 If ui.y = T.y
{
PUSH(Q,ui);
WhichChain <-- U;
T_changes <-- TRUE;
}
3.3 If li.y > T.y
If l(i-1).y < T.y (* there is proper intersection *)
{
V <-- Intersection point of SEG(l(i-1), li) and y=T.y;
PUSH(Q,V);
PUSH(Q,li);
WhichChain <-- L;
T_changes <-- TRUE;
}
Else
{
PUSH(Q,li);
WhichChain <-- L;
T_changes <-- TRUE;
}
3.4 If ui.y < T.y
If u(i-1).y > T.y (* there is proper intersection *)
{
V <-- Intersection point of SEG(u(i-1), ui) and y=T.y;
PUSH(Q,V);
PUSH(Q,ui);
WhichChain <-- U;
T_changes <-- TRUE;
}
Else
{
PUSH(Q,ui);
WhichChain <-- U;
T_changes <-- TRUE;
}
3.5 If (WhichChain = L) AND T_changes
{
T <-- li;
Last.y <-- li.y;
}
Else If T_changes
{
T <-- ui;
Last.y <-- ui.y;
}
T_changes <-- FALSE;
END (* for *)
PUSH(Q,Last);
S = Q;
End (* algorithm *)
Complexity
The test for monotonicity (step 1) can easily be done in O(n)
time by a while loop.
Step 3 is a simple for loop, and all the statements in the body, including
computing the intersection point can be done in constant time. Note also that
only the push operation is performed on the stack. Thus the total time
complexity of the algorithm is O(n).
Correctness
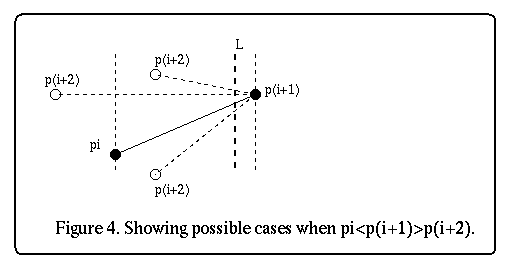
In step 1, if pi.xp(i+2) then P is not monotonic in the x direction.
Note that the vertices of P are labeled from left to right. Figure 4 shows
what happens.
In step 3, the algorithm checks all of the following cases (figure 5):
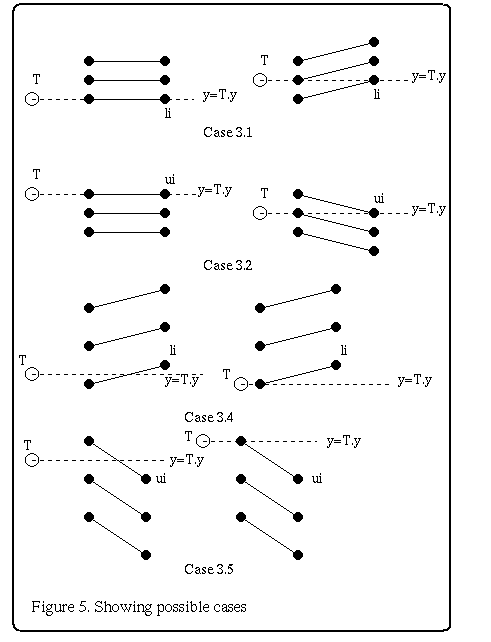
A moment's thought reveals that this are the only possible cases worth checking.
Thus, when the algorithm terminates, the stack Q contains all the points of
the smoothed chain, S, with the first point pushed being s1 and the last pushed
being sk (2 <= k <= 2n -1). The last two points may be identical, but this
does not pose any problems. Note that S may contain more points than the
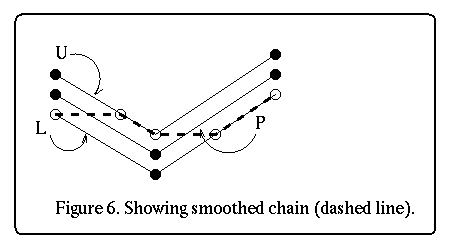
original chain P, see figure 6. Clearly, this algorithm does not perform
data reduction as its primary goal and may not be useful in applications which
data reduction is critical. Also, extending this algorithm to non-monotonic
polygonal chains is not trivial.
Inputting Polygonal Chains and The Threshold
Points are input by clicking the left mouse button in the applet's area.
They are joined automatically by line segments in the order they were input.
Clicking the middle or right mouse button signals the end of input.
The threshold value t is entered by using the scroll bar at the top of
the applet's area. The default value for t is 25 units.
Running The Algorithm
Press the Compute button to run the algorithm on the input chain.
The RED chain is the resulting hysteresis-smoothed chain.
To test different values of the threshold t on the same polygonal chain,
press the Clear New Chains button to delete all the new chains
displayed except the input chain. Then change the threshold by using the
scroll bar and running the algorithm again.
 Home Page
Home Page
Copyright © 1997 T.Z. Nkgau. All rights reserved.



 Lastly, connect u1 and l1 to p1, un and ln to pn, to form a monotonic polygon in
Lastly, connect u1 and l1 to p1, un and ln to pn, to form a monotonic polygon in



 Home Page
Home Page