Proof :
This is easily proved : a line going from a vertex b of a
triangle abc to some point that belongs to the opposite side
ß
is always shorter than one of ab or cb, or both.
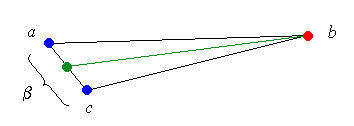
So if some point x of ß is the furthest point of A from b, then x has to be an endpoint of ß, and thus a vertex of A.
Q.E.D.
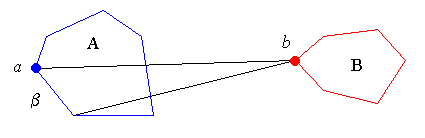
Notice however that lemma 2 applies only to a, the furthest point of A relative to b : as illustrated below, the closest point b of B relative to a might not be a vertex of B.
