Updating triangulations.
Updating Triangulations.
(Insertions and Deletions of edges and vertices.)
Computational Geometry, 308-507 Term Project, Sergei Savchenko.
1. Introduction.
Given a set of points in the plane, A triangulation of , denoted , is a graph with P as its nodes and edges connecting the nodes so
that as many triangles as possible are formed and the edges intersect only
in the nodes (see Figure 1.0).
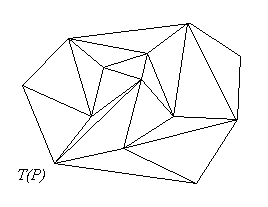
Figure 1.0.A triangulation of a set of points.
Triangulations occur very often in such diverse areas as cartography
(approximation of surfaces), computer graphics (shape representation),
stress analysis (finite element models) etc.
Although the problem of constructing a triangulation given a set of points
or a simple polygon has been paid considerable attention, at times, in
various contexts, it is also necessary to update existing triangulations
by inserting or deleting some vertices or edges. Some strategies to do
that are considered in this page.
2. Nodes.
In the vertex insertion problem we want to construct a where is some new point. Two cases are possible:
If is located outside the convex hull of it
can be joined to all the visible nodes on the convex hull. To do that we
construct the upper and lower lines of support connecting the convex hull
vertices with the point being inserted and then interconnect all vertices
on the inner part of convex path thus formed with the point (see Figure 2.0 B).
If is located in the interior of the convex hull of
it must lie inside some triangle
of . In which case, it is, possible to connect
to the vertices of obtaining a valid
triangulation (see Figure 2.0 A, point ).
Alternativelly, some inserted point may happen to overlay
some edge. For this particular problem such a degeneracy can be
trivially handled by splitting the edge at the inserted vertex and
adding another new edge into every triangle the original edge was a
member of (see Figure 2.0 A, point ).

Figure 2.0. Inserting a vertex into a triangulation.
In the vertex deletion problem we must compute a triangulation of
where . Discarding an
internal point along with all edges originating in
leaves a star-shaped hole
(see the Appendix) which can be efficiently
triangulated using the three-coins algorithm
(see Figure 2.1 A).
Note that we can easily create the list of the vertices on the boundary
of the hole by traversing the triangles of the triangulation (Assuming,
of course that an efficient data-structure which chains all triangles
is used).
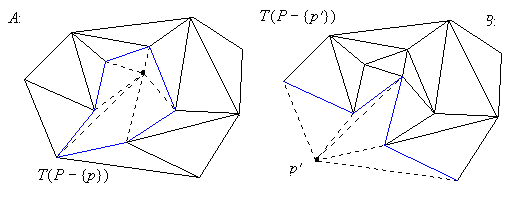
Figure 2.1 Deleting a vertex from a triangulation.
In another instance of the deletion problem we may have to remove a
vertex on the convex hull (see Figure 2.1 B). In this case, we don't
normally obtain a star-shaped hole, but some externaly
visible boundary (all deleted triangles shared the same vertex and thus
any edge on the boundary is visible from that vertex). It is sufficient
to apply the three-coins algorithm to this boundary
which will both compute the necessary fragment for the convex hull of the
entire triangulation and at the same time externally triangulate all
pockets (see Appendix).
The following applet demonstrates inserting and deleting vertices
from triangulations (click onto previously inserted vertex to delete it):
The source code is available.
3. Edges.
The edge insertion problem can be described as follows: Given a finite
set and
its triangulation we want to find another triangulation
such that an edge exists between the specified pair
of nodes. In other words, insert an edge into the triangulation
. Or, with another problem, given the same input
we want to compute a triangulation in which the
specified two nodes are not joined by the edge, that is, delete an
edge from the triangulation .
The following subsections discuss different cases of edge insertion/deletion.
3.1 Inserting an edge into a triangulation.
Depending which nodes are specified for edge insertion two different
cases are possible:
- Connect with an edge two nodes and
in the case when both belong to the set
(Insert an "open" edge).
- Connect with an edge two nodes and
in the case when both don't
belong to the set (Insert a "closed"
edge).
3.1.1 Inserting an open edge.
In the case when both nodes to be connected by an edge are already members
of the set we first discard all other edges of the triangulation
which are intersected by the edge we insert. This can be
done in linear time and it produces two edge-visible
polygons (see the Appendix). Note that these
polygons can be constructed very efficiently by traversing triangles in the
triangulation (assuming that every triangle is chained to its neighbors).
These polygons are edge visible since they are formed of triangles, all
intersected by the same edge. Any point on the internal boundary must, thus,
be visible from this edge. Such regions can be efficiently triangulated by
the three-coins algorithm in linear time (see Figure 3.1).
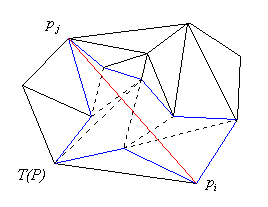
Figure 3.1. Inserting an open edge into a triangulation.
3.1.2 Inserting a closed edge.
When the nodes to be connected by an edge don't belong to the set
, such a problem is trivially reducible to the open
edge problem by inserting the nodes first, updating the triangulation
accordingly and then invoking the open-edge insertion
computation described in the previous section (see Figure 3.2).
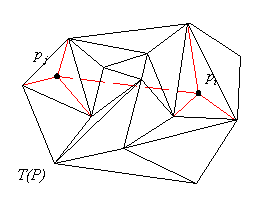
Figure 3.2. Inserting a closed edge into a triangulation.
3.2 Deleting an edge from a triangulation.
Similarly to the insertion problem, we can differentiate several cases
of the edge deletion problem:
- Delete an edge along with its end-points:
and (delete a "closed" edge).
- Delete (if possible) the edge connecting some nodes , but leave the end-points in the
set (delete an "open" edge).
3.2.1 Deleting a closed edge.
Obviously, for the closed edge deletion problem all we have to do is to
first delete one of its end-points (see Section 2), triangulate the resulting
star-shaped hole (or externaly-visible region in the
case of convex hull vertex), remove the other end-point and finish by
triangulating the second hole or region. As a result,
we obtain a valid triangulation lacking both two deleted
nodes and their connecting edge.
Although this computation takes linear time, we may do somewhat
better by avoiding triangulation of two star-shaped
holes (together resulting in application of three-coins
algorithm up to six times) and directly construct some
edge-visible holes requiring only four application of the triangulation
algorithm.
Thus we start by extending the edge we want to delete, find its
intersections with some other edges on the boundary of the formed
hole. Further, we insert these Steiner points into the set, triangulate
the formed edge-visible polygons, remove the Steiner
points and obtain other edge visible polygons which can be trivially
triangulated (see Figure 3.3).
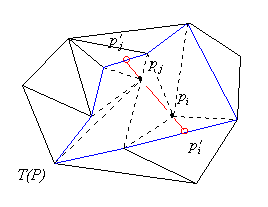
Figure 3.3. Deleting a closed edge from a triangulation.
3.2.2 Deleting an open edge.
The open edge deletion problem requires, if possible, to produce an
updated triangulation in which the two nodes
, previously
connected by an edge are no longer connected.
Clearly, this may not always be possible (see Figure 3.4 A). Edge
cannot be deleted from the triangulation .
To delete an open edge we must find two other points from the set
, and
whose connecting line (a stabbing line) intersects the edge
we want to delete. Insertion of an edge necessarily deletes the edge
solving the open edge deletion problem.
One straightforward way of finding a stabbing line is by checking all pairs
of points from the set to verify if any intersects the
edge we want to delete. To speedup this quadratic computation we can
precompute the required information ( whether the edges intersect ) in a
square array, use it to fetch stabbing edges in unit time and make sure
we adjust the array according to the triangulation updates.
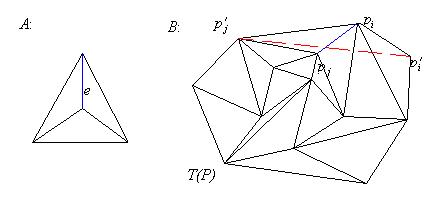
Figure 3.4. Deleting an open edge from a triangulation.
The following applet demonstrates inserting and deleting edges from
triangulations. First mouse click selects one end point of an edge,
marked by a blue square, the second click specifies the other endpoint.
The operation (deletion/insertion) is choosen based on the context, except
to differentiate between types of deletions which should be preselected
in the check-box.
The source code is available.
4. Appendix:
Three-coins algorithm.
The three-coins algorithm was proposed by J. Sklansky for finding a
convex hull of a simple polygon (for which task it is incorrect),
and by Graham as a final step in finding convex hull of a set of
points (for which it does work).
Although this algorithm fails in finding a correct convex hull of
a general simple polygon, it does work for an important class of
polygons, notably those which are weakly externally visible.
A polygon is called weakly externally visible if any point
on its border is directly visible from some point located at infinity.
This algorithm can be described as follows:
for n points of a polygon: k,k+1,...,k+n-1, starting with k=0 which
is assumed to be convex.
do
if (k,k+1,k+2) are counterclockwise triple and k+2=n then stop
else
if (k,k+1,k+2) are counterclockwise then move one point forward
else
begin
delete k+1, add diagonal (k,k+2)
if k=n then move one point forward
else move one point backward
end
end
The algorithm proceeds by finding and closing with a lid
each encountered pocket (see Figure 4.1).
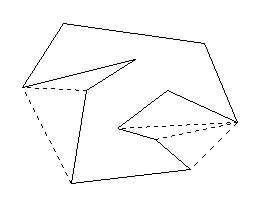
Figure 4.1 Applying the three-coins algorithm.
Paraphrasing, if the algorithm encounters a concave vertex it proceeds
forward, when it encounters a reflex vertex it cuts it and performs
backtracking step.
Note that in the process of finding a lid each of the pockets has been
externally triangulated.
The suggested algorithm, however, assumes that no three vertices in the
polygon are collinear. In the presence of such degeneracies a modified
version of the three-coins algorithm should be used.
for n points of a polygon: v,k,k+1,...,k+n-2,u such that
uv is the visibility edge, and a stack S so that s is stack's top.
push v
push k
assign x=k+1
do
if x=v stop
if (s-1,s,x) are counterclockwise or 0 degree turn triple then
begin
push x
move x one point forward
end else begin
if (s-1,x,x+1) is a 180 degrees turn then
then add diagonal (s,x+1), move x one point forward
else add diagonal (s-1,x), pop stack
end
if s=v then
begin
push x
move x one point forward
end
end
Note that the presence of collinearities allows for two types of
degenerate triangles to be produced by the original, unmodified,
version of the algorithm: those having 0 degrees turn and 180 degrees turn.
Whereas handling the former is easy enough by only a slight modification,
it is mostly the latter which causes the changes.
Triangulating edge-visible polygons.
A polygon is called Edge-visible if there
exists an edge so that any point inside the polygon is visible
from some point on this edge.
Since the three-coins algorithm was capable of externally triangulating
the pockets (which are edge visible polygons with respect to the lid)
we can internally triangulate any edge-visible polygon using the above
algorithm in linear time (see Figure 4.2).
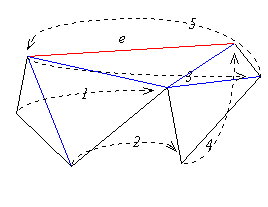
Figure 4.2 Triangulating an edge-visible polygon.
Triangulating star-shaped polygons
A polygon is called Star-shaped if there
exists some point so that any point inside the polygon is visible
from this point. The set of all such points is called the
Kernel of the polygon.
If we are given a point in the kernel such polygons can be triangulated
using a variation of the three-coins algorithms. Notably we want
to first insert an edge originating in some vertex and passing through
the kernel. This edge may intersect some other edge on the other
side at which place we will introduce a Steiner point. The resulting two
edge-visible polygons can be efficiently triangulated (the newly
inserted visibility edge passes through the kernel and hence all
points in both halves are visible).
Afterwards, we remove the Steiner point and invoke the three-coins
triangulation once again to fill the formed hole which was edge
visible since the removed point was originally placed onto an edge
(see Figure 4.3).
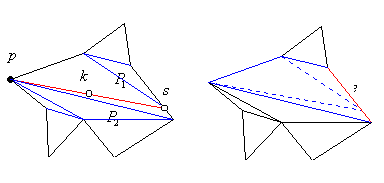
Figure 4.3 Triangulating a star-shaped polygon.
5. References.
-
[1] H.A. ElGindy, G.T. Toussaint, "Efficient algorithms for inserting
and deleting edges from triangulations." Proc. International Conference
on Foundations of Data Organisation, Kyoto University, 1985.
-
[2] G.T. Toussaint, D. Avis, "On a convex hull algorithm for polygons and its
application to triangulation problems," Pattern Recognition, Vol. 15,
1982, pp. 32-29.
-
[3] A.A. Schone, J. van-Leeuwen, "Triangulating a star-shaped polygon,"
Technical Report RUV-CS-80-3, University of Utrecht, April 1980.
-
[4] R.L. Graham, "An efficient algorithm for determining the convex
hull of a finite planar set," Inform. Process. Lett. 1, pp. 132-133, 1972.
-
[5] J. Sklansky, "Measuring concavity on a rectangular mosaic,"
IEEE Transactions on Computing. C-21, pp. 1355-1364, 1972.
-
[6] P. Bose, G.T. Toussaint, "Growing a tree from its branches,"
Journal of Algorithms. 19, pp. 86-103, 1995.
Last updated 12/28/97.
Comments about the page?
Download this page.










