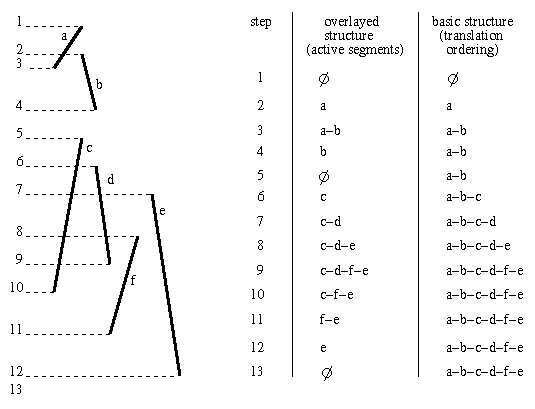Relation ixdom+ is the transitive closure of ixdom.
We say that segment s1 is below s2, iff the y value of the lower end point of s1 is less than the y value of the lower end point of s2.
See Figure below:
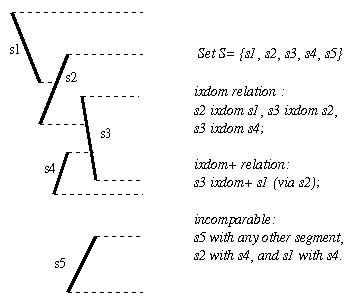
The desirable ordering dom is obtained by choosing
for each pair of segments the ordering from ixdom or below:
s1 dom s2 iff (s1 ixdom+ s2) or (not(s2 ixdom+ s1) and (s1
below s2)).
The computation of the segment ordering is determined
by the relation dom by an horizontal
scan line sweep from top to bottom which stops at each end point of a segment.
We define 2 data structures:
- one basic structure, where all segments encountered so far are stored in reverse ixdom+ | below ordering.
- one overlaid structure for the active segments only, that is the segments actually cut by the scan line.
Description of the algorithm:
Sort the end points of all segments according to their
y values in descending order.
Initially, the basic structure and the overlaid structure
are both empty.
For all end points in descending y order
do:
If the point is an upper end
point of a segment s,
then
search for the active successor s' of s in the overlaid
structure;
if s' exists,
then insert s as the new predecessor of s' in the
basic
structure and in the overlaid one.
else insert s as the new final element in the basic
structure
and as the rightmost element in the overlaid structure.
else delete
s from the overlaid structure (but not from the basic
structure).
The basic structure gives then the translation ordering starting from the end.
Example of processing: