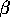-Neighbours
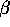-neighbours in the set
S if N(x,y,
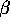) contains no point of S, other than x or y, in its
interior. There are various kinds of definitions of N(x,y,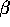
). One of
them is called Lune-Based Neighbourhoods.
Lune-Based Neighbourhoods
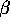) for various 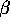>0
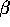
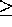1
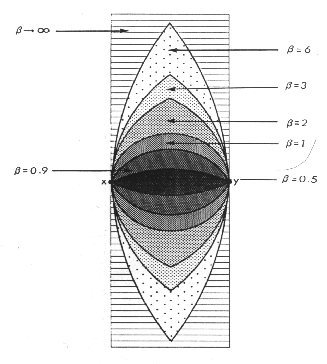
We difine N(x,y,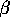
) to be the intersection of the two circles of
radius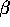 
d(x,y)/2 centered at the points (1- 
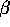/2)x+(
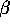/2)y and
(
/2)x + (1-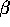 
/2)y, respectively.
When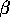 
=1, N(x,y,
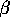) corresponds exactly to
the Gabriel neighbourhood
of x and y. When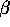 
=2, we get the ``relative neighbourhood'' of the RNG.
As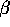 
approaches 
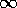, the neighbourhood of x and y approximates the
infinite strip formed by translating the line segment (x, y) normal to itself.
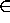[0,1]
We difine N(x,y,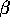
) to be the intersection of the two circles of radius
d(x,y)/(2
) passing through both x and y. When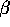 
=1, this is
consistent with the definition abvove. As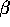 
approaches 0, N(x,y,
)
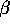approximates the line segment joining x and y. Thus, except in degenerate
situations (three or more points colinear), all point pairs are
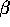-neighbours under this scheme for 
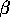sufficiently small.
go back to Beta Skeleton go back to Home 
Xiaoming ZHONG