The Algorithm of Rosenfeld

The algorithm described here is a simple parallel algorithm due to Rosenfeld.This algorithm works by successively discarding in a parallel fashion subsets of the "boundary" of P.We first define the word of boundary. Let P be, the set of black (one's) pixels. The complement of P is the background (such pixels are white(zero's)). Consider a pixel p1 of P. Label the 8 neighbors of p1 as shown below :

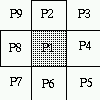
p1 is a north border point if p2=0.

p1 as a north border point
p1 is an east border point if p4=0.

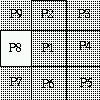
p1 as an east border point
p1 is a west border point if p8=0.

p1 as a west border point
p1 is a south border point if p6=0.

p1 as a south border point
p1 is a 4-endpoint provided that exactly one of its 4-neighbors is black.

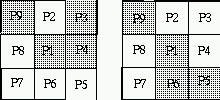
Two examples where p1 is a 4-endpoint point
p1 is an 8-endpoint provided that exactly one of its 8-neighbors is black.

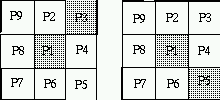
Two examples where p1 is an 8-endpoint point
p1 is a 4-isolated point if none of its 4-neighbors is black.

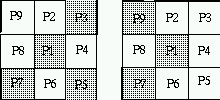
Two examples where p1 is a 4-isolated point
p1 is an 8-isolated point if none of its 8-neighbors is black.

Here p1 is an 8-isolated point
A border point p1 is a 4-simple if changing it from black to white (one to zero) doesn't alter the 4-connectivity of the remaining black pixels within the Moore neighborhood of p1
Here there are two examples which are not 4-simple :

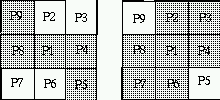
Two examples where p1 is not a 4-simple point
A border point p1 is an 8-simple if changing it from black to white (one to zero) doesn't alter the 8-connectivity of the remaining black pixels within the Moore neighborhood of p1
Here are two examples which are not 8-simple :

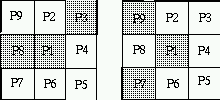
Two examples where p1 is not an 8-simple point

Now we are ready to describe the algorithm which can be viewed in two different modes depending on the type of connectivity used.These algorithms are in part sequential and in part parallel.

ALGORITHM 4-CONNECTED

begin
repeat until no pixels are changed from black to white:: step 1 :(in parallel)Change all black pixels to white if they are north borther points that are 4-simple but neither 4-isolated nor 4-endpiont.; step 2 :(in parallel)Change all black pixels to white if they are south borther points that are 4-simple but neither 4-isolated nor 4-endpiont.; step 3 :(in parallel)Change all black pixels to white if they are east borther points that are 4-simple but neither 4-isolated nor 4-endpiont.; step 4 :(in parallel)Change all black pixels to white if they are west borther points that are 4-simple but neither 4-isolated nor 4-endpiont.
end repeat
end

ALGORITHM 8-CONNECTED

begin
repeat until no pixels are changed from black to white:: step 1 :(in parallel)Change all black pixels to white if they are north borther points that are 8-simple but neither 8-isolated nor 8-endpiont.; step 2 :(in parallel)Change all black pixels to white if they are south borther points that are 8-simple but neither 8-isolated nor 8-endpiont.; step 3 :(in parallel)Change all black pixels to white if they are east borther points that are 8-simple but neither 8-isolated nor 8-endpiont.; step 4 :(in parallel)Change all black pixels to white if they are west borther points that are 8-simple but neither 8-isolated nor 8-endpiont.
end repeat
end

The order of the sequential part of algorithm,i.e.,the north, south, east, west sequence for examining border points is arbitrary but should be consistent.It also helps to alternate in this way in order to obtain skeletons that are centered in the original pattern.

An important property of this algorithm is that it preserves the connectivity of the input pattern.

Home