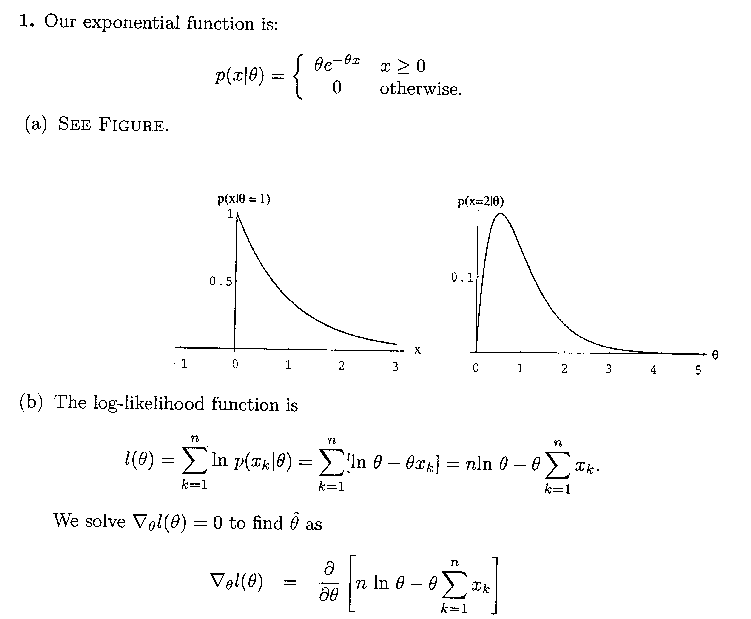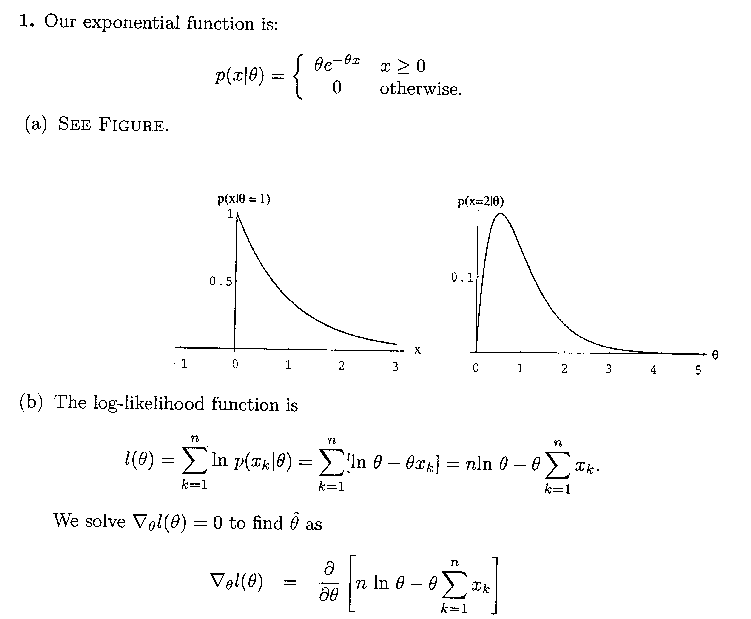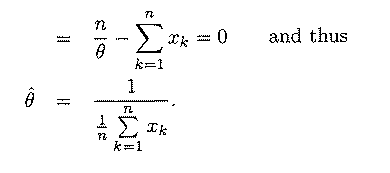Problem 1




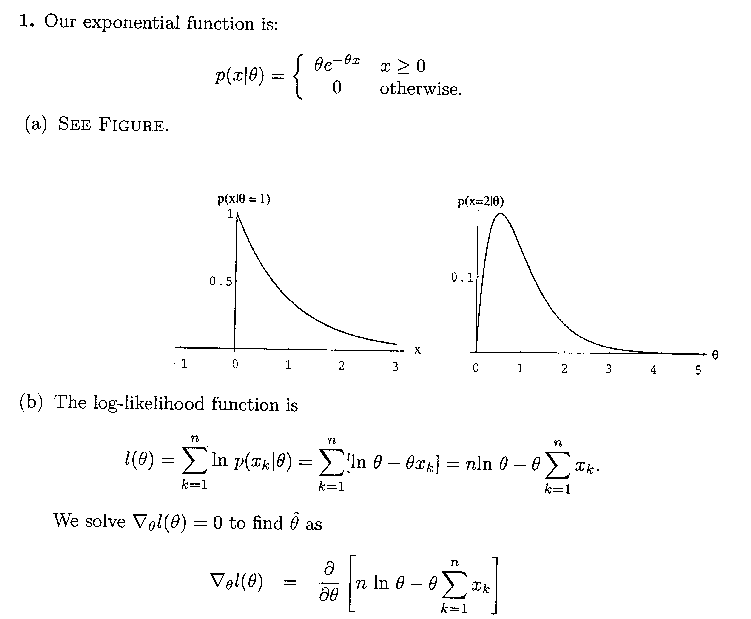
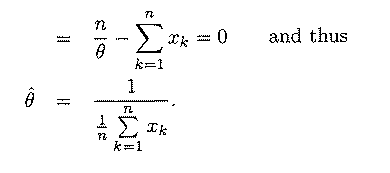
Problem 2

Part (a)

It's easiest to think of this problem geometrically. We have one interval 0 <= x <= (CR/(C-1)) where each class has equal density throughout, and i disjoint intervals where only one class per interval has nonzero density.

Thus, we have two cases when given a vector x to classify:

Case 1: x lies in 0 <= x <= (CR/(C-1)).
Since all densities are equal, a random guess as to which class x belongs is as good a guess as any. So our Bayes chance of error given that x lies in this interval is (C-1)/C.
Case 2: x does not lie in 0 <= x <= (CR/(C-1)).
Then x lies in an interval where only one class has nonzero density, so the Bayes chance of error here is zero.
Every class has density 1 in the interval 0 <= x <= (CR/(C-1), so whatever class x really is, it has a (CR/C-1) chance of landing in this interval. This is the only interval which allows Bayes error, so

Pe(Bayes) = [P(x lies in this interval)] * [Pe in this interval]
Pe(Bayes) = [CR / (C-1)] * [(C-1) / C]
Pe(Bayes) = R

If you feel more comfortable with the algebra,

INTEGRAL -inf+inf   p(x) * [1 - max(P(Ci|x)] dx

Since either p(x) or [1 - max(P(Ci|x)] is zero everywhere except 0 <= x <= (CR/(C-1), this is equal to

INTEGRAL0CR/(C-1)   p(x) * [1 - max(P(Ci|x)] dx

which equals [CR / (C-1)] * [(C-1) / C] = R by the same math as above.

Part (b)

Suppose we have infinite data. Again, we have two cases.
Case 1: x lies in 0 <= x <= (CR/(C-1)).
Since all densities are equal, the nearest neighbour to x will be equally likely to be in any class. So our 1-NN chance of error given that x lies in this interval is (C-1)/C.
Case 2: x does not lie in 0 <= x <= (CR/(C-1)).
Then x lies in an interval where only one class has nonzero density. Since the intervals i + 1 - (CR/C-1) do not touch (i.e., there is nonzero distance between them), the nearest neighbour of x will lie in this interval and therefore be of the same class. The 1-NN error here is zero.
It's the same logic as before:

Every class has density 1 in the interval 0 <= x <= (CR/(C-1), so whatever class x really is, it has a (CR/C-1) chance of landing in this interval. This is the only interval which allows 1-NN error, so

Pe(1-NN) = [P(x lies in this interval)] * [Pe in this interval]
Pe(1-NN) = [CR / (C-1)] * [(C-1) / C]
Pe(1-NN) = R
Problem 3

I assume that I have infinite data. I also need the assumptions that I now show that Pr(2-NN) = Pe(1-NN).

Let X1 and X2 be the two nearest neighbours of X. 2-NN Rejection occurs if X1 and X2 are of different classes, and 1-NN error occurs if X and X1 are of different classes.

Pr(2-NN) = [P(C1|X1) * P(C2|X2)] + [P(C2|X1) * P(C1|X2)]

Pe(1-NN) = [P(C1|X) * P(C2|X1)] + [P(C2|X) * P(C1|X1)]

Since I chose X, the density there is non-zero and continuous. Thus I choose any neighbourhood of X and have infinite data. Thus X1 and X2 are arbitrarily close to X. Since the densities are continuous, p(C1|X) = p(C1|X1) = p(C1|X2); likewise for C2. Thus,

Pr(2-NN) = [P(C1|X1) * P(C2|X2)] + [P(C2|X1) * P(C1|X2)]
Pr(2-NN) = [P(C1|X) * P(C2|X)] + [P(C2|X) * P(C1|X)]
Pr(2-NN) = 2 * [P(C1|X) * P(C2|X)]

Pe(1-NN) = [P(C1|X) * P(C2|X1)] + [P(C2|X) * P(C1|X1)]
Pe(1-NN) = [P(C1|X) * P(C2|X)] + [P(C2|X) * P(C1|X)]
Pe(1-NN) = 2 * [P(C1|X) * P(C2|X)]

Pr(2-NN) = Pe(1-NN)

Now I must show that Pe(2-NN) <= Pe(Bayes). 2-NN error occurs if X1 and X2 are in different classes than X.

Pe(2-NN) = [P(C1|X) * P(C2|X1) * P(C2|X2)] + [P(C2|X) * P(C1|X1) * P(C1|X2)]
Pe(2-NN) = [P(C1|X) * P(C2|X) * P(C2|X)] + [P(C2|X) * P(C1|X) * P(C1|X)]
Pe(2-NN) = [P(C1|X) * P(C2|X)²] + [P(C2|X) * P(C1|X)²]

Suppose that P(C1|X) <= P(C2|X). Then Pe(Bayes) = P(C1|X).

Pe(2-NN) = [P(C1|X) * P(C2|X)²] + [P(C2|X) * P(C1|X)²]
Pe(2-NN) = P(C1|X) * {P(C2|X)² + [P(C2|X) * P(C1|X)]}

But we can show that P(C2|X)² + [P(C2|X) * P(C1|X)] <= 1.

P(C2|X) <= 1
P(C2|X) - P(C2|X)² <= 1 - P(C2|X)²
P(C2|X) * (1 - P(C2|X)) <= 1 - P(C2|X)²
P(C2|X) * P(C1|X) <= 1 - P(C2|X)²
P(C2|X)² + [P(C2|X) * P(C1|X)] <= 1

Thus Pe(2-NN) <= Pe(Bayes). It may seem odd that a decision rule can have a smaller error rate than Bayes, but remember that the 2-NN rule isn't classifying everything, since it doesn't classify what it rejects. In other words, the 2-NN refuses to classify "difficult" data. If you assume that half of the rejects will be errors, you'll see it is higher than Bayes. Anyone can do better than Bayes if you skip the difficult data . . .


Problem 4

Part (a)

The two classes occur in unit hyperspheres ten units apart. Suppose we have m data of class A, and n data of class B. If I give you a new element that falls in the hypersphere of class A, then we know it's a class A instance because the space of A and the space of B are disjoint. So apply the nearest neighbour rule, as the question asks. The first m nearest neighbours (quite close, within unit distance) are of class A, and when those are exhausted, the next nearest data are of class B, ten units away. Thus error occurs under the k-NN rule only if m < k/2, and our query occurs in the set with m elements. What is the chance that, given equal a priori probabilities, that we picked such a distribution for the training set? It's like making n coin flips and having fewer than k/2 come up as heads -- and then being asked to classify a coin flip of heads.

It's exactly the equation in the problem.

Part (b)

Same reasoning; if k = 1, then m = 0. This is more unlikely than m < k/2 for k > 1.


Problem 5

Part (a)

I'll let you be the artists here . . .

Part (b)

It's the same rule. If I use the k-NN rule, then take a majority vote of the k nearest neighbours (k odd). Suppose class A wins the vote. Then certainly the (k + 1)/2 - th instance of A was closer than the (k + 1)/2 - th instance of B; otherwise there would have been more B's than A's among the k nearest neighbours! The converse logic is similar, so we have an if and only if.