Solutions are by Mike Soss.
Problem 1
Here is a counter-example.
Run the Ramer-Douglas-Peucker algorithm on this chain with the specified tolerance, w.
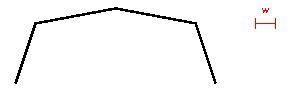
We start with:

The middle vertex is the farthest from the green approximation, so we obtain:

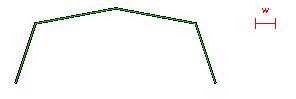
Now each of the other vertices are also too far away from the green approximation. Therefore, we repeat
the algorithm on each subchain. We get:
But all along, this magenta chain has fewer vertices, and stays within the error tolerance.
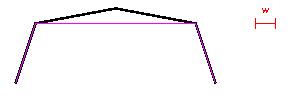
If you didn't get it, a valid question might be, "How did you think of this one?" Well, once the
RDP algorithm selects any vertex farthest from the green approximation, it stays in the approximation
forever. All you have to do is create a chain where the first vertex which is farthest from the green
line is not in the optimal approximation.
Problem 2
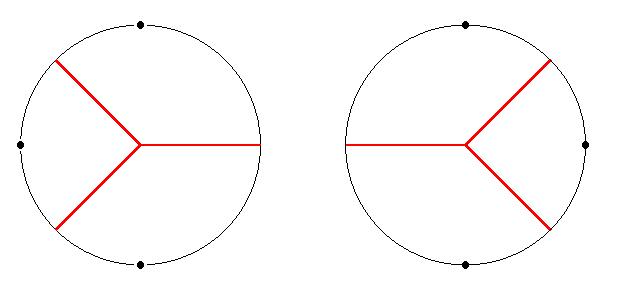
Here is a clear counterexample. P appears on the left; its antipodal set on the right. Medial axes are in red.
Problem 3
Hilditch's algorithm is based more on just hacking to see what works as opposed to real theory.
So given his rules, just try to construct a pattern that "fools" all of them.
Run Hilditch's algorithm on the pattern below, and, well, you'll see . . .

There are families of patterns which will foil Hilditch's algorithm, including one which looks like a diagonal line.
See if you can find it.
Problem 4
Here's a quick, easy proof.
We wish to prove that:
limp -> inf [|x|p + |y|p]1/p = max{|x|, |y|}
First, note that
max {|x|p,|y|p} <= |x|p + |y|p <= 2 max{|x|p, |y|p}.
Since
max {|x|p,|y|p}1/p = max{|x|, |y|},
we get
max {|x|,|y|} <= [|x|p + |y|p]1/p <= 21/p max{|x|, |y|}.
So what happens when p gets very large? Well, (1/p) approaches zero, so 21/p approaches 1.
So the left and right sides of the previous inequality are equal! If A <= B <= A then A = B, so
limp -> inf [|x|p + |y|p]1/p = max{|x|, |y|}.







