Given the perspective projection example below, it is too ambiguous to tell whether it is a set of four disjoint segments, or a cube, or a square. Here we introduce the term 'regularity', trying to define a nice perspective projection that will find a projection with little ambiguity.

Figure 1 four disjoint segments or a cube or a square?

In this session, there are two main issues we are concerned about:

1. Decide whether a projection is a regular perspective projection

2. Find a projection that satisfy regularity

First, let's look at the formal definition of regular projection. Next, we explain these two problems in details.

DEFINITION 1. Let S be a set of disjoint segments in space. A perspective projection of S is said to be regular when the following three conditions are fulfilled:

1.- no point of the projection plane is the projection of more than one endpoint of segments of S;

2.- no point of the projection plane is, simultaneously, the projection of an end-point and an interior point of two segments of S;

3.- no point of the projection plane is the projection of more than two interior points of segments of S.

Simply speaking, this definition of regularity means: 1) a line segment should not be diminished to a point in the projection, otherwise breaks the condition 1. 2) an endpoint of a line segment should not be connected to another line segment in the projection, otherwise breaks the condition 1 and 2. 3) no more than two intersections should occur in the projection, otherwise breaks the condition 3.

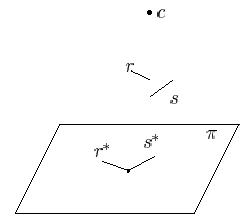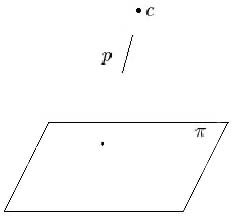
Figure 2 breaks condition 1	Figure 3 breaks condition 1

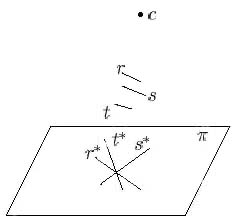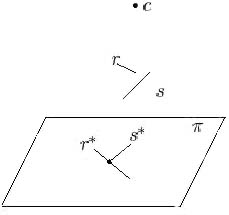
Figure 4 breaks condition 2	Figure 5 breaks condition 3

1. Decide whether a perspective projection of n disjoint segments is a regular perspective projection

Let S be a set of disjoint segments. A point that can not be the projection center of a regular perspective projection of S is called a forbidden point ( see figure 2). So to decide whether the perspective projection of n disjoint segments reduces to the problem of deciding whether the projection center is the forbidden point. Actually the projection centers in figure 2 to figure 6 are all forbidden points.

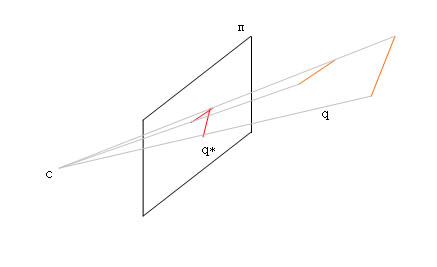
Figure 6. A forbidden point

Observation:

There are two cases that a point will be a forbidden point. First, if a point and one of the endpoint of the disjoint segment are on the same line l, then it is a forbidden point. Secondly, a point lies on a line l that simultaneously intersects more than three segments. Actually, all the points on this line l are forbidden points. We can see, the conditions of regularity only depend on the projection center and not on the projection plane.

2. Find a projection that satisfies regularity

Definition: The transversal line of one segment is the line containing it. The transversal lines of two segments form four double wedges; each wedge is obtained by taking all the lines that go through an endpoint of a segment and through any point of the other segment. (See figure 7)

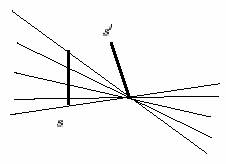
figure 7 double wedge

Pseudocode:

Input: segments set S

1. Translate the coordinate system oxyz to cxyz, so that all endpoints of segments have coordinates strictly positive and no plane defined by and a segment of S contains the axis cx.

2. If c is not a forbidden point then exit

3. Compute the intersection of each of the O(n) lines that contain the segments with axis cx

4. Compute the intersection of each of the O(n2) double wedges of forbidden points with the cx axis

5. Choose point i which is among the intersection points and closest to c but not equal to c

Output: point i and point c