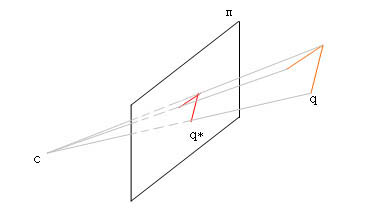
Perspective Projection: A perspective projection in space is determined by the projection center c, and a projection plane pi. The perspective projection of a point q is the intersection q* of the line qc with the plane pi.

Note: The projection plane doesn't pass through the projection center. The points of the plane pi_c which go through c and is parallel to pi cannot be projected onto pi.

Figure 1. Perspective Projection

Nice Perspective Projection : A projection that gives an image in which the features of the object are visible without ambiguity. To achieve this, we need to check regularity, minimum crossing, and monotonicity of the projection.

Regularity, minimum crossing and monotonicity are three separate definitions for nice perspective projection. Sometimes a perspective projection can satisfy regularity but breaks minimum crossing or monotonicity. And sometimes the perspective projection can satisfy minimum crossing but fails in monotonicity or regularity. But there are still two things always being true:

1.When the number of the intersections of the minimum crossing of the perspective projection equals to zero, the perspective projection is also a regular projection.

2. When the perspective projection is a monotonic projection, then it is also a regular and minimum crossing projection.

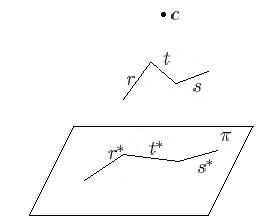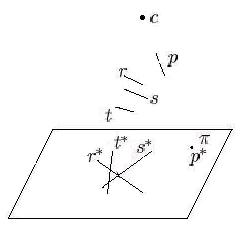
Figure 2 Regular but not minimum crossing and not monotonic	Figure 3 Monotonic and also regular and minimum crossing