In some medical applications, we may have a 3-D directed tree as an object of interest. Such a tree may represent a system of veins in the human brain for example, where the direction of an edge represents the direction of blood flow in the corresponding vein segment. It is of interest to determine if there exists a projection such that all the directions of the edges of the tree are monotonically increasing in a specified direction on the projection plane. That is why we introduce another way to obtain a nice perspective projection, which is called monotonic projections. More specifically, a projection is monotonic if the projected image on the projection plane is monotonic. A planar polygonal chain is monotonic if there exists a direction such that every line orthogonal to this direction, that intersects the chain, yields no more than a point as the intersection.

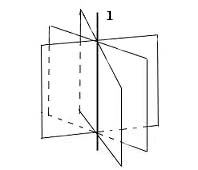
Definition 1: Given a line l, the pencil of planes that goes through l will be denoted by H(l).

Figure H(l)

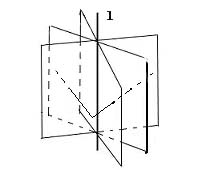
Definition 2: A simple polygonal chain in space is said to be strictly monotonic with respect to a line l when the intersection of the polygonal chain with any plane of H(l) is the empty set or a point.

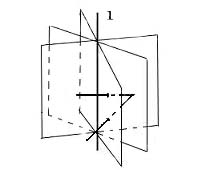Figure 2 Monotonicity	Figure 3 Non-Monotonicity

Observation:

Observe that if P is strictly monotonic with respect to line l, then l can not intersect the convex hull of the chain P, because on the contrary there always exist a plane of H(l) that intersects P in two points.

Suppose, given a projection plane, and the projection center c on a line l, if we move the line l to infinity, then the pencil of planes will become parallel and orthogonal to the projection plane. Let n be a vector in the projection plane and orthogonal to the direction vector of the straight line l, then we obtain the definition of monotonicity of a perspective projection.

Definition 3: Let P be a simple polygonal chain in space. A perspective projection P* of P is said to be monotonic when the polygonal chain P* is strictly monotonic with respect to some direction n of the projection plane.

Why in the definition we say 'some direction n' instead of specifying it? Because, the direction n depends not only the on the position of the projection plane but also the direction of the direction of the line l. Without specifing the line l, we can not decide the direction of n.

Observation:

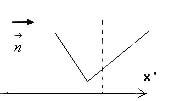
Suppose the direction of n is a new axis x', if no two projection points P* of the polygonal chain P share the same coordinate x', then the perspective projection P* of P is said to be monotonic with respect to the direction of n.

Figure 4 P* is monotonic to direction n	Figure 5 P* is non-Monotonic to direction n

The monotonicity is very sensitive to the direction n.

Theorem 1 If the polygonal chain p is monotonic with respect to a line l, then the polygonal chain P* of the plane pi is strictly monotonic with respect to the direction n.

Proof

Prove by contradiction: Let P be a strictly monotonic polygonal chain with respect to an oriented line l. Let c be a point of l and let pi be a plane that separates l and P. P* is the perspective projection of P on plane pi. n is a vector in the plane pi orthogonal to the direction of l. Suppose P* is not monotonic with respect to the direction n. That means we can find a line r orthogonal to n and intersects two edges of P* at the points e* and f* respectively. Let e and f be, respectively, the points of P whose projections are e* and f*. Under these conditions, the plane pi(r) in H(l) (that is, pi(r) is a plane that cross both line r and line l) intersects the simple polygonal chain P in e and f. Therefore the chain P is not strictly monotonic with respect to the line l contradicting our hypothesis.

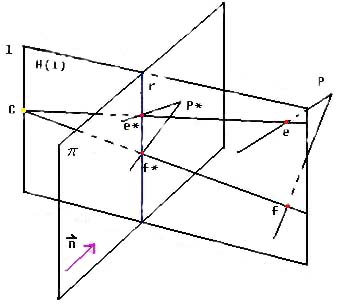
Figure 6 prove by contradiction