When viewing a 3D simple polygonal chain based on perspective projection, in order to obtain a nice 2D image of the 3D object without ambiguity, one interest is to let the number of the intersections of the projected lines in the image to be as less as possible.

Sometimes, the number of the intersections could be zero, which is the best situation. But sometimes, there does not exist a projection center that will make the number of intersections of the projected segments be zero. For example, see the figure below. In this situation, to find the projection centers that minimize the number of the intersections is the goal.

Figure 1 a top view of veins in the brain

In this session, there are three issues we are concerned about:

1. Decide whether a projection is simple projection

2. Find a projection that is a minimum-crossing projection

3. Find a minimum-crossing projection with the restriction that the projection center lies on a line segment

First, let's look at the formal definition of simple projection and minimum-crossing projection. Next, we explain these three problems in details.

Definition 1: Let S be a set of disjoint segments in space. The perspective projection of S is said to be minimum-crossing when the number of crossings of the projected segments of S is minimum.

Definition 2: If the minimum number of crossings is zero, we call such projections simple or crossing free.

Example:

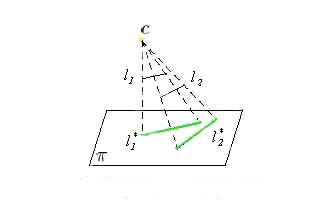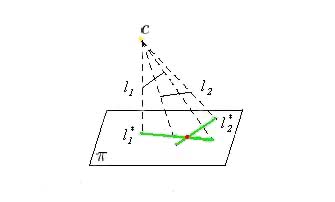
figure 1. not simple segment projection	figure 2. simple segment projection

In the figure 1, as l1 intersects with l2, it is not a simple segment projection.

1. Decide whether a projection is simple projection

Suppose is the set of projected lines of . In the Figure 1 and Figure 2, we can see , and . It is obvious to see that to decide whether the projection of projected semgments of is simple, we just need to decide if any two of the n projected segments of intersect. If the number of the intersections is zero, then it is a simple projection, whereas, it is a non-simple projection.

Complexity In [15], it presents an algorithm that can detect if any two segments of n segments intersects in time and space.

2. Find a projection that is a minimum-crossing projection?

We have discussed in Regular Projection, when the projection center c belongs to a transversal of two segments of S the point c is a forbidden one. Here, let T(s, s') be the set of transversals of the segments s, s' < S. T(s, s') is a region. Figure 3 shows T(s,s').

Figure 3 Region T(s,s')

We can see, if the projection center is in the region T(s, s'), then the projected line of segments s and s' must be intersected in the image plane. For any two segments of S, we can construct a region T(s, s'). Totally, we may construct O(n2) regions. If the projection center are in one of theses O(n2) regions, then the projected line of the two segments that construct this region intersect in the image plane. Otherwise, none of projected line of any two segments intersects in the image plane. The problem of deciding if a simple perspective projection of S exists can be transformed to the problem deciding if the O(n2) regions determined by every two segments cover the space.

Denote by T the contour of the union of those regions, a simple perspective projection of S exists if and only if T does not cover the space. In this case, if we take any point c in the complement of T as the projection center, we will obtain a simple perspective projection of S. If O(n2) regions cover the whole space, in order to determine the center of projection c of the minimum-crossing perspective projection of S, we can choose a point c covered by the minimum number of such regions.

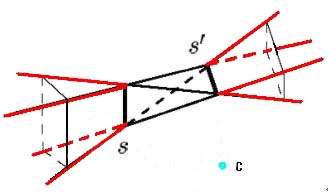
Figure 4 choose a point c in the complement of T

Pseudocode:

Input: segments set S

1. Construct T(s, s') for each two segments s and s'

2. For each pair of segments in S, determine a plane, let P be the whole sets of this planes

3. Using the algorithm described in [4], arrange P to decide the regions divided by P in the space;

     Let A(P) be the arrangment of P

4. For each cell of A(P), compute the T(s, s') regions that contain it

5. Using depth-first search to find the cells C of A(P) covered by the minimum number of T(s,s')

Output: cells C

Complexity:

For step 1, using the algorithm discussed in [3], it can be obtained in O(n2). For step 2, it can be done in O(n2). For step 3, described in [4], it can be finished in O(6). For step 4, as there are O(n2) regions, it can be done in O(n2). For the last step, it can be done in O(n6). So the whole process to find the minimum-crossing perspective projection can be done in O(n6) time.

From problem 2, the complexity of finding the minimum-crossing perspective projection is O(n6), which is not an effective way. If we give some restriction to the positions of the projection center, the time complexity could be decreased. In the paper, it restricts the projection center lies on a line segment.

3. Find a minimum-crossing projection with the restriction that the projection center lies on a line segment

With constrain, the projection center must lie on a given line segment. Then the points of the segment l covered by the minimum number of regions T(s, s') produce perspective projections of S with the minimum number of crossings. The intersection of l with each T(s,s') gives one or two sub-segments of l. There are O(n2) regions T(s,s'). We compute the intersection of l with each regions T(s, s'), then we obtain a set L of O(n2) sub-segments in O(n2) time.

In order to find the points of l covered by the minimum number of T(s, s') regions, we can sort the set E of endpoints of the segments of L in O(n2logn) time. By traversing the O(n2) points of E in order, we find the parts of the sub-segments of L covered by the minimum number of T(s,s') regions. Then the projection center of the minimum-crossing projection will fall on those segments.

Pseudocode:

Input: segments set S

1. Construct T(s, s') for each two segments s and s'

2. For each T(s, s'), calculate its intersection with line l,

       Store the intersections as the endpoints of the new sub-segments

3. Sort the endpoints

4. Traversing the endpoints, find sub-segments set L covered by the minimum number of T(s, s')

Output: sub-segments set L

Complexity:

For step 1, using the algorithm discussed in [3], it can be done in O(n2). For step 2, as there are O(n2) regions T(s, s'), calculating the intersections can be done in O(n2). For step 3, sorting the endpoints can be done in O(n2logn). For step 4, traversing the endpoints and find the sub-segments set L can be done in O(n2). So, given a set of n disjoint segments in space, finding a minimum-crossing perspective projection, with the restriction that the projection center lies on a line segment, the whole process can be done in O(n2logn) time and O(n2) space.