


Next: Crossing-free
Projections
Up: Projections
Previous: Projections
Regular and Wirtinger Projections
It would be nice if all the significant features of the 3D objects are
visible in the projections.
In the projection of a polygon, we do not expect some vertices or edges
disappeared. Let S be a set of n distinct points and disjoint line
segments in the space, and H be the plane where
we will operate the projection. Let SH be the parallel
projection of S onto H.
Definition: A parallel projection of S is said
to be regular if no three points of S project to the same point
on H and no vertex of S projects to the same point on H as any other
point on S.
The following picture shows three different projections of a cube, one
of them is not a regular projection.
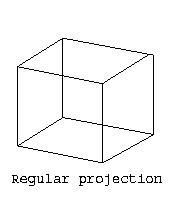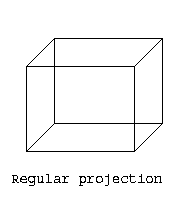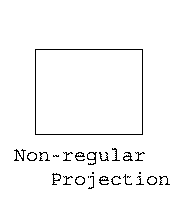
For a regular projection of disjoint line segments, we may conclude
from the definition:
- No point of SH corresponds to more than one vertex of
S.
- No point of SH corresponds to a vertex of S and an
interior point of an edge of S.
- No point of SH corresponds to more than two interior
points of edges of S.
Hence, the only crossing points we will find in a regular projection,
will come from the intersection of the interiors of two edges of S.
Thinking about it, you will see that almost every polygon has a regular
projection.
Nevertheless, a regular projection may lose some important information
of the original object.
Let's have a look at the next picture.
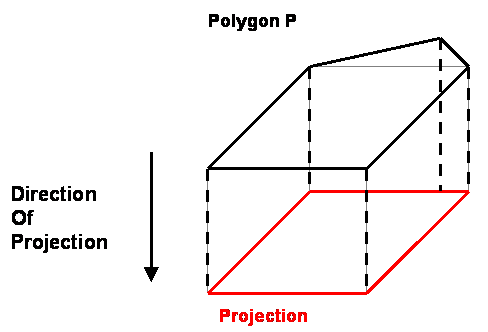
It is indeed a regular projection, but two edges have collinear
projections.
Thus we lose precious information about the shape of the polygon.
That kind of loss is not good for visualisation, so we introduce a
restricted class of regular projections
called Wirtinger projections, for which no two consecutive
edges of the 3D polygon have
collinear projections.



Contact us :
Jean HERBIERE
and Yueyun SHU


