Monotonic Projections

Next: Monotonicity Issues Up: Projections Previous: Crossing-free Projections

Monotonic Projections

We arrive now at the main part of our survey, the monotonic projections.

Definition: A projection is said monotonic if all the directions of the edges are monotonically increasing in a specified direction on the projection plan.

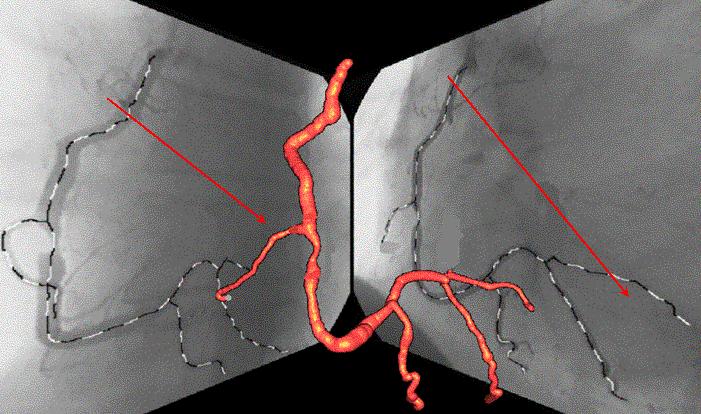
Projections that preserve monotonicity of trees find applications in medical imaging. Let's think about arteries and veins, the visualisation is far more easy if they run in a single direction. Our purpose is to find projections which conserve this property of monotonicity in some directions and to identify them.

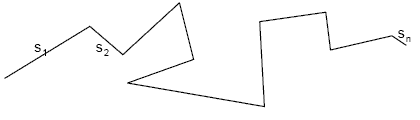
Our objects of interest at here are polygonal chains and trees, let's see what they look like.

Definition: A polygonal chain is set of line segments s₁,s₂,...,s_n such that s_i is connected to s_i+1 at their common endpoint for i between 1 and n and two segments intersect each other only at their endpoints (s₁ and s_n do not intersect).

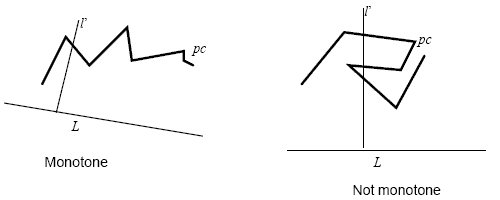
A polygonal chain, pc, is monotone if there exists a line L such that all lines l' perpendicular to L intersect pc at most once.

And for the trees:

Definition: A tree is a mathematical structure which can be viewed as either a graph or as a data structure. (here we deal with the tree graph.) A tree graph is a set of straight line segments connected at their ends containing no closed loops (cycles).

See more detailed definition on MathWorld or Wikipedia.

Finally, a polygonal chain or a tree may not admit a crossing free projection, but it may admit a projection which is monotonic in some direction. We can observe two projections of a vein on the following picture, and both have definitely a projection monotonic in one direction shown in red arrow.

We will see in the next chapter the main issues and complexity of finding monotonic projections.

Jean HERBIERE and Yueyun SHU