Introduction

Next: Projections Up: Home Previous: Home

Introduction

We live in a 3D (three-dimension) space, what we see everyday, like street, building, trees, etc., are all in 3D. Although our eyes can percept 3D objects naturally, it is not convenient to describe everything with a real 3D object. In fact, we often describe things on a 2D medium, such as paper or screen. Things are projected from 3D to 2D in this situation. Any photo we shot is a projection in 2D; any movie we watch is a projection of a 3D scene on a screen.

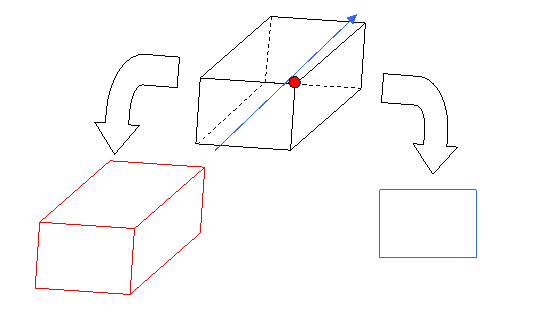
There are two types of projections we often use: perspective projections and parallel (orthogonal) projections. Here we deal with the latter. When doing a projection, we will lose some information. Our goal is to obtain 2D representations that approximate the real objects as faithfully as possible in some sense. Intuitively, we may think of our objects as a wire-frame sitting in 3D space above the horizontal xy-plane, and the parallel projection of the object on the xy-plane as the shadow cast by the wire-frame when a light source shines from a point infinitely high along the positive z-axis. Obtaining "nice" parallel projections of an object then reduces to the problem of finding a suitable 3D rotation for the object such that its shadow on the xy-plane contains the desired properties. Here is an example of two different projections of a simple cuboid.

How will we proceed?

First we are going to introduce three types of parallel projections that have been well studied in graph drawing area. Then, we will focus on a specific projection, called monotonic projection, to see what they are useful for, and how we can obtain this kind of projections, as well as the complexity of the algorithms.

Jean HERBIERE and Yueyun SHU