What, are you having trouble giving me an answer? Then take a guess. Chances are, close to 50% of you answered yes, and the other 50 answered no. Of course, given no other information about my state right now, it would be difficult for you to make a decision. There is an equal probability for me to have the flu or not. You might need to make an observation first. For example, if I tell you that my temperature is 42 degrees. I ask you again, Do I have the flu?
Bayes decision making is about making a decision about the state of nature based on how probable that state is. In the above example, you want to decide whether to diagnose me with the flu based on how probable it is that I have it. Given that my temperature is high, the odds of me having the flu are now higher, but still not 100%, since it can be due to other diseases for example. Thus, the observation of my temperature gives you a better idea about my state. Once we have obtained an observation x, we can have a better idea about the state of nature. Thus, the probabilities of the current state of nature have changed due to our observation.
In the above example, w1 is the state of having the flu and w2 is the state of not having the flu. As we saw, the probability of ![]() (p(
(p(![]() )) has changed given the observations (i.e. p(
)) has changed given the observations (i.e. p(![]() )
) ![]() (
(![]() |x) ). If p(
|x) ). If p(![]() |x) > p(
|x) > p(![]() |x), then the probability of the patient having the flu is higher than the probability of the patient not having the flu, and you might be inclined to decide that the patient has the flu. Of course, if you want to be just a bit more careful you might want to run some medical exams before making such a diagnosis, but let’s not complicate things. If you decide on
|x), then the probability of the patient having the flu is higher than the probability of the patient not having the flu, and you might be inclined to decide that the patient has the flu. Of course, if you want to be just a bit more careful you might want to run some medical exams before making such a diagnosis, but let’s not complicate things. If you decide on ![]() , there are chances that you make the wrong decision. The probability of making the wrong decision is the same as the probability that nature is at a different state that the one we chose, that is the probability that the patient doesn’t have the flu. In the case of deciding on
, there are chances that you make the wrong decision. The probability of making the wrong decision is the same as the probability that nature is at a different state that the one we chose, that is the probability that the patient doesn’t have the flu. In the case of deciding on ![]() , the error is the probability of state
, the error is the probability of state ![]() given the observation x (p(
given the observation x (p(![]() |x)).
|x)).
Formally, the probability of error is:
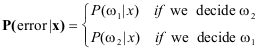
So if we decide wi and p(![]() | x) > p(
| x) > p(![]() | x), then we get a higher error than if we decide
| x), then we get a higher error than if we decide ![]() . Thus deciding on the state that has the higher posterior probability minimizes the probability of error.
. Thus deciding on the state that has the higher posterior probability minimizes the probability of error.
If we generalize to more than 2 possible states, and replace the observation x with a vector X, minimizing the error rate corresponds to the following decision rule:
Decide ![]() if P(
if P(![]() |x) > P(
|x) > P(![]() |x) for all j
|x) for all j ![]() i
i
The continuous case involved features vectors that could be any point in Rd. For example, a feature can be the temperature of a room and can have any value, including decimals. The discrete case basically involves a limited or finite number of possible observations. Thus, the feature vector x is no longer element of Rd. But can now have m possible discrete values v1,…vm. For example, a feature can be the state of a switch that can either be on (1) or off (0). This leads to a few minor changes in the way the decision rule is calculated, as we will see below.
|
|
is replaced by |
|
|
where we sum the conditional probabilities for all possible values of x in the discrete distribution. |
|
|
|
instead of |
|
|
| where |
|
(for j possible states.) |