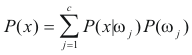
For pattern recognition tasks, many times the data that is required to be analyzed and classified is a discrete vector of (sometimes assumed independent) components: X = (x1,x2,x3,...,xn). This vector is usually found by some type of pattern recognition algorithms. To make a decision on a feature vector in the discrete case, we must first investigate Bayes rule in discrete form.
As was seen in the continuous case of Bayes rule, the discrete case is much similar. However, instead of the feature vector x being a point in d-dimensional space, it now assumes one of m discrete values: v1,...,vm. Consequently, integrals are therefore replaced with summations:
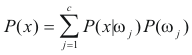
Furthermore, instead of utilizing probability density functions as was used if the random variable was continuous, the distribution is now a probability distribution or just a probability. Hence:
![]()
Nonetheless, as will be seen, the Bayes decision rule remains unchanged as it’s purpose is: to minimize the risk or cost in the decision.