|
Planar Shape Recognition By Shape
Morphing
|
|
| |
|
The General Idea... |
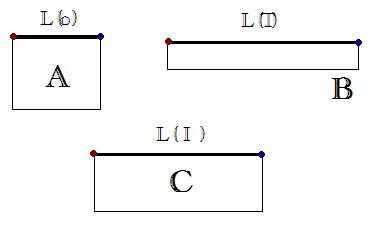
For humans, it is relatively easy to distinguish and classify an object, according to the visual information we obtain from looking at the object. For example most people would be able to distinguish an apple from an orange easily, or the sun from the moon. However, for a computer this is a very complex task. The idea here is to use shape morphing to gather the necessary information that will allow a computer to classify a shape according to the shapes that that the computer already has in its database. For example, if we have the following three shapes in the database:
and a user drew the following shape, User drawn image then we would want our program to match it to the purple arrow, and not any of the other shapes in our database, even though it is rotated 90 degrees and a different color. Shapes are represented by their contours. Using the contour information a morph is performed between the user drawn shape and the template objects (target shapes) stored in the database. The cost of a morph is measured with a physics-based method, and the morph that produces the smallest cost in the deformation of the original object to an already existing object in the database, is chosen as the closest match. The user drawn object is then classified as this template. If this seems like an innovative method of pattern recognition to you, then read on!
For a pattern recognition algorithm to be successful it should follow the following properties, which were presented by Arkin et al. (as taken from [1]):
This method manages to encompass all of these properties as well as:
The authors chose to represented shapes by their contours. The contour of a shape is taken to be outer hull of the object.
The contour is chosen for a number of reasons:
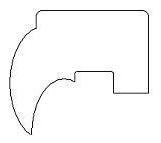
However, it is not the entire contour that we are really interested in since there can be a huge number of points on the contour of an object, and finding a correspondence between them could require a large amount of computation (I will talk more about what a correspondence is soon). What we really want, are the points where the object has large minimums and maximums, or the areas where the object bends and folds (in essence we want to find the corners of the objects, or the points which make the object unique). We will then use this approximation of the shape as our object contour. For example, the interesting points of the above contour are illustrated by the small square in the image below:
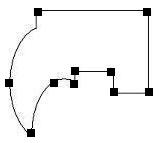
Our polygon contours are represented as a sequence of points and lines in our java applet. (See java applet for more information). A shape is then segmented using a polygon segmenting algorithm to find the areas of interest and to reduce the number of points that will be involved in the morphing process. Once the polygon has been segmented, we are left with a new polygon approximation of the original polygon. Back to Index
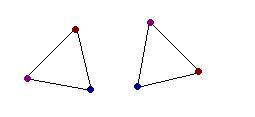
The word morph is short for metamorphoses, which means to change from one state to another. We are using a morphing process specifically to gather information that will allow our program to recognize an object and to classify it according to existing objects already contained in a database of shapes. The morph proceeds by deforming (stretching and bending) the source polygon (inputted by the user) until it matches the target polygon (contained in the database of shapes). A morph is created between the user drawn shape and each template object in the database. In order to create a morph between the source and target contours, the algorithm first needs to specify a correct correspondence between the key points obtained in segmentation of the source and target contours. This is done by mapping, the key points on the contour of the source object with those on the target polygon. In the example below, we have a point correspondence specified by the color of the points on the corners of the triangles. The point correspondence is formulated in such a way that the morph that will ensue between the the input and target shape will have the smallest cost.
However, it needs to be stated that two shapes, the input shape and the target shape, may not have the same number of segmentation points. If this is the case then two points (or more) in the source contour can map to the same point in the target contour. Once a correspondence is created, then a cross-dissolve plus a warp is used to formalize the morph. Below is an example of one of the morphs that the authors generated using this algorithm.
To obtain the best possible point correspondence possible between the source and target polygon they used a physics based approach which measures the amount of stretching and bending required to morph the source contour into the target contour. For each pair of points (or triplets of points) in the correspondence they use the following formulas to compute the amount of stretching and bending energy. To compute the amount of stretching energy required to morph the source into the target the following is used: .jpg)
where:
The above formula measures the amount of stretching energy between each pair of line segments specified by the point correspondence. The total amount of stretching energy needed to create the morph is the sum of all the stretching energies summed over all line line segments. To calculate the amount of bending energy, the following formula is used: where:
The above formula measures the amount of bending energy required between each triplet of points in the point correspondence and computes the cost of the angular deformation of the contour. Similar to the way that the the total amount of stretching energy was computed, we compute the total amount of bending energy required by taking the sum over all point correspondences. To test all the different possible point correspondences, an exhaustive search method is employed, and then the best result form all these is used. The point correspondence that yields the smallest values in both E(s) and E(b) is chosen as the optimal one, since it is the morph between the two polygons that requires the least amount of stretching and bending to create the morph. Once we have the best point correspondence between the user drawn object and each template in the database, the template that would create the smallest morphing cost (and hence has the smallest E(s) and E(b) over all objects in the database) is chosen as the object which the user drawn template will be classified as. Since this is the object that requires the least amount of deformation between it and the user drawn image, it is therefore (by this measurement), the most similar to the user drawn image. To summarize the overall recognition process, it is done as follows:
In this paper it is interesting to note that the results of the algorithm will only be as good as the segmentation algorithm used to select the key points from the original contour. In there experiments, misclassification was usually caused by improper selection of the feature points of the contour. It also must be said that because objects and sketches are morphed using only the contours of the object, if the object is shaded in any way, or if there is poor illumination on the object then the algorithm will break down since an improper contour of the object would be obtained for the shape. They tested the algorithm in three different
cases: 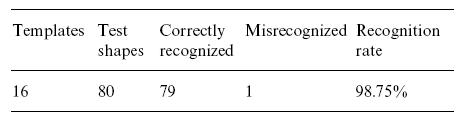 Case 2: Recognition of Deformable Shapes Deformable shapes were classified as hand-drawn outlines of objects, sketches of natural images, and contours obtained from real-world objects. 15 shapes were used in total, and 4 sketches of each shape were stored in the database as templates for a total of 60 objects to choose from. To conduct this experiment, people were shown what sketches were in the database briefly, but then had to sketch their own representation of the object without the templates in front of them. In this way, the results in the table below were obtained.  Case 3: Recognition of Unconstrained Cursive Handwriting For this experiment they used 10 randomly chosen words and each user provide one template sample to store in the database for a total of 40 words per user in the database. They also asked each user to provide 4 test samples of the each of the 10 words to test the recognition algorithm with. The table below shows the results of these experiments. 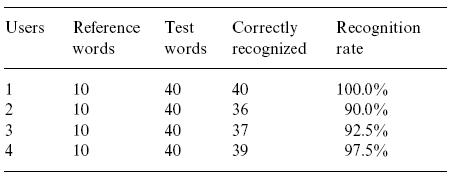 Back to Index
|