Let's consider a process of building a classifier that uses Bayes decision rule. See Erin Mcleish tutorial for a nice introduction on Bayesian classifiers and decision rules. Given a feature vector x, we compute the a posteriori probability P(w|x) for every class and make the decision in favor of the class maximizing this value. By Bayes rule, the a posteriori probability can be expressed as
![]()
where P(w) is an a priori probability, p(x|w) is the
state-conditional probability density function and p(x) can be regarded as a
constant which does not influence the decision. When we talk about classifiers
and decision rules, we usually regard the a priori probability and the
state-conditional probability values as known or available. In practice,
however, it is rarely the case. As there is no way we can obtain the exact
values of these probabilities, we use samples to compute their estimates. While
estimation of the a priori probabilities P(w)
does not usually present a problem (simple count of samples can be used), we'll often run into difficulties when
trying to estimate the class-conditional densities due to insufficient number of
samples. If we don't have any prior knowledge about class-conditional density
distribution the task of its estimation is rather unfeasible. Fortunately, quite often
we can make certain assumptions about the shape of the distributions, which will
facilitate estimation process. It's quite common to assume that the
class-conditional densities p(x|w) have normal distribution.
In this case, the problem of estimating the probability densities is
reduced to the problem of estimating the parameters of normal
distribution, namely the mean
![]() and the
covariance matrix
and the
covariance matrix
![]() . In case of d-dimensional feature vector, the
. In case of d-dimensional feature vector, the
![]() is a d-dimensional vector and
is a d-dimensional vector and
![]() is
a square matrix of dimension d. So the number of parameters to be estimated is
d+d(d+1)/2.
is
a square matrix of dimension d. So the number of parameters to be estimated is
d+d(d+1)/2.
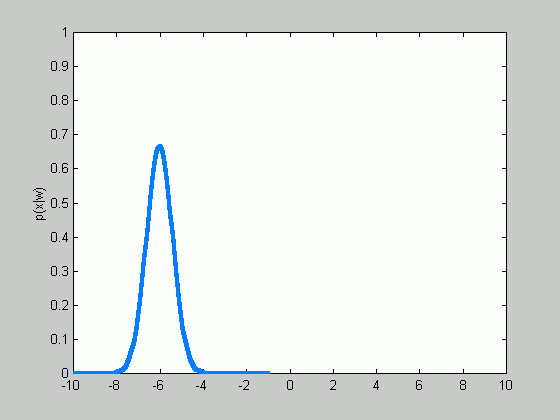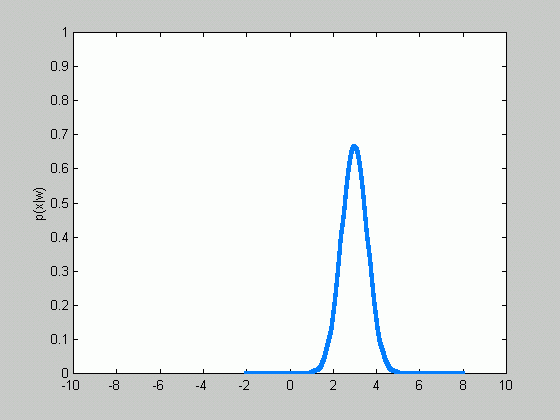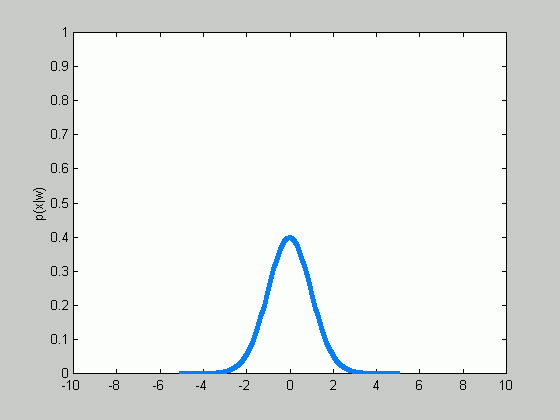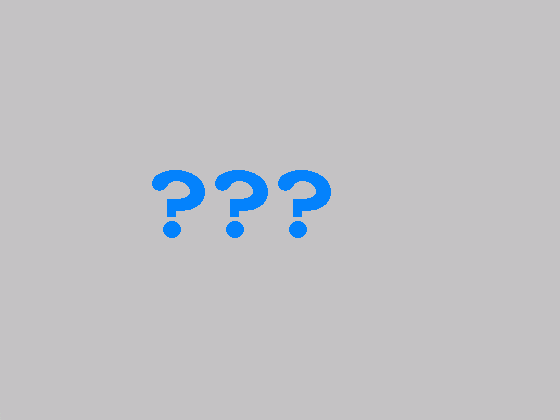
Sometimes, we can facilitate the problem even
further. There are case when the covariance matrix is known in advance.
Therefore, only the mean
![]() is
to be estimated.
is
to be estimated.
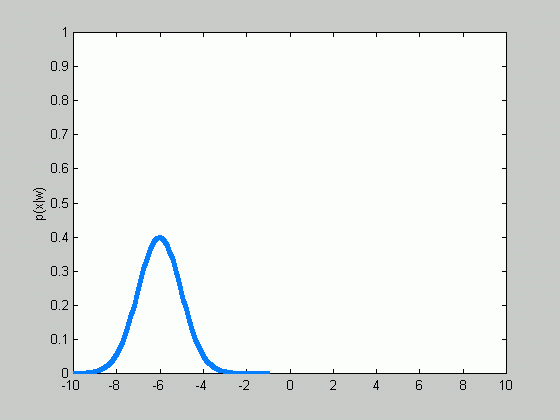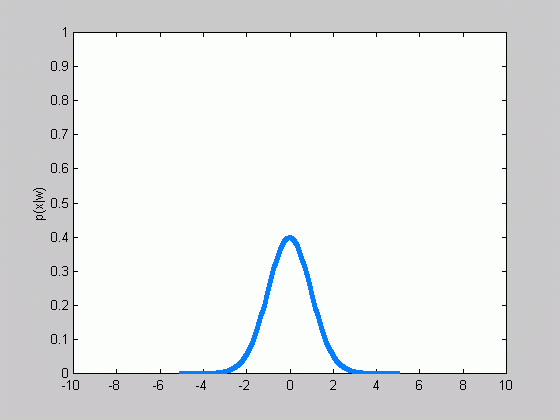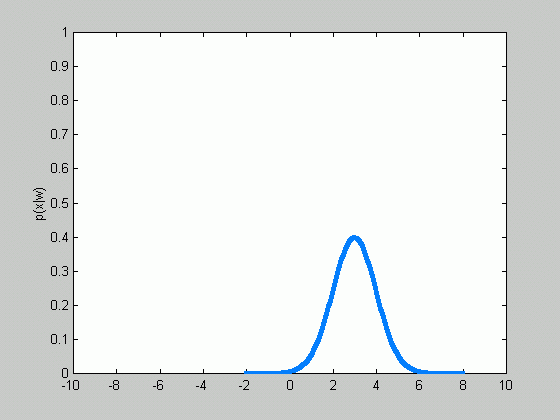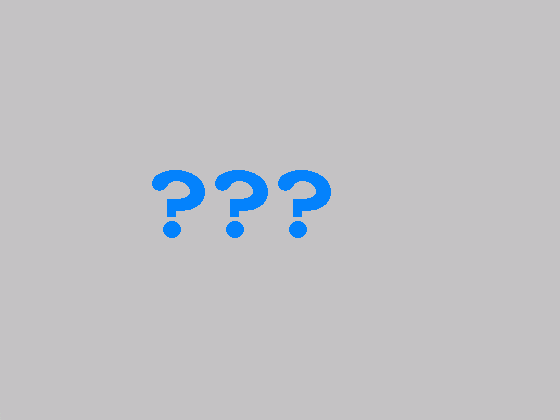
There are two classical approaches to the parameter estimation problem. The first, maximum likelihood, treats the parameters as unknown but fixed values, and the estimate is defined to be the values which maximize the probability of obtaining the samples observed. The second, Bayesian approach, is quite different. It views the parameters as random variables rather then fixed values. This tutorial is mostly dedicated to the Bayesian approach. Besides giving a presentation to the approach in general, we'll have a detailed look at the case when the class-conditional density is assumed to have normal distribution, when the covariance matrix is known and the mean is to be estimated.