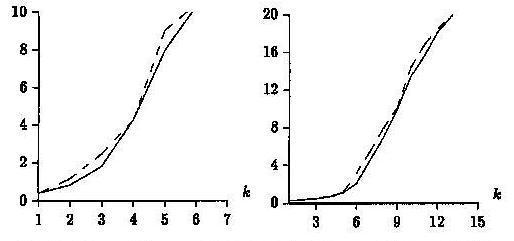
 Figure 3.
Figure 3. The optimized (solid line) and the normal splitting (dashed line), for
m = 10 (left) and 30 (right) on English text.
Optimizing the Partition
The choice available when partitioning
the pattern into k + 1 pieces can be used to minimize the expected number
of verifications by using the occurrence frequency of letters in the alphabet
under consideration(and this is not limited to the English alphabet).
Once the probability of an occurrence of each letter in the alphabet is
known, the probability of the occurrence of a substring can be computed
by simply taking the product of the occurrence probabilities of the letters
that make up the substring. Thus if we wish to know the occurrence probability
of the substring "yes", and we know the probability of 'y' is, 0.1, 'e'
is 0.3, and 's' is 0.3, then the probability of that substring being verified
is (0.1)X(0.3)X(0.3) = 0.009. This probability of a sequence can be used
in inbuilding the tree, as a partition that minimizes the sum of the probabilities
of the pieces is desired, since this is directly related to the number of
verifications that will be carried out.
This leads to the folllowing dynammic programming algorithm:
Let R[i,j] = r=iΠ j-1Pr
(pat[r]) for every 0 ≤ i ≤ j ≤ m. It can be
observed that R can be computed in O(m2) time since
R[i, j+1] = R[i,j] X Pr(pat[j]).
Using R we build two matrices,
P[i,k] = sum of the probabilities of the pieces in the best partition
for pat[i...(m-1)] with k errors.
C[i,k] = where the next piece must start in order to obtain P[i,k].
This requires O(m2) space, and
the following algorithm computes the optimal partition in O(m
2) time. The final probability of verification is P[0,k],
and the pieces start at L0 = 0, L1 = C[L0
, k ], L2 = C[L1, k-1], ..., L
k = C[Lk-1, 1].
for( i = 0 ; i < m ; increment i by 1 each iteration)
P[i,0] = R[i,m];
C[i,0] = m;
for(r=1; r ≤ k ; increment r by 1 each iteration)
for(i=0; i < m - r; increment i by 1 each iteration)
P[i,r] = minimum((R[i,j] + P[j, r - 1])) for all j in the interval [(i+1), ..., (m-r)]
C[i,r] = j that minimizes the expression
above(that is, it minimizes P[i,r])
The speedup obtained by implementing this modification
to the partition is very slight, and sometimes even counterproductive, since
it only takes the probability of verifying a letter sequence into consideration.
The search time of the extended algorithm degrades as the length of
the shortest piece is reduced (as in an uneve n partition), and so a cost
model that is closer to the real search cost is considered by optimizing
1/(minimum length) + Pr(verifying) X m2.
Figure 3 (above) shows the result of running 100 experiments
on English text using the optimized and normal splitting methods, each using
the original verification method and not the hierarchical one. The
small degree of improvement is visible in both runs, and is especially noticeable
in the medium error range (upper right on both graphs).

