Preparata & Shamos 1985

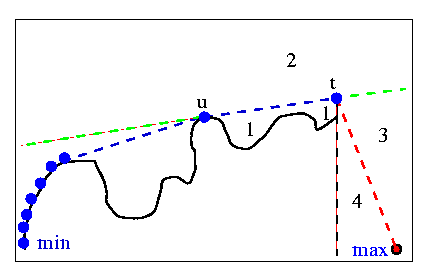
In their book [14], Preparata and Shamos present their "original variant of Lee's algorithm". There really isn't much of a difference from Lee's algorithm (or from the Graham-Yao algorithm) , apart from some details. The authors show how to compute the upper hull, between Xmin and Xmax. Given a stack which contains the vertices accepted so far, the authors divide the plane into 4 regions.

Let (t) be the top of the stack, (u) be the vertex underneath it in the stack, and (t-1) be the vertex prior to (t) on the polygon.

Region 1 is inside the last "pocket", to the right of the line from (u) to (t), and to the left of the line from (t-1) to (t).

Region 2 is "above" the last convex hull line accepted, i.e. to the left of the line from (u) to (t).

Region 3 is to the left of the line from (t) to Xmax, and to the right of the line from (u) to (t).

Region 4 is to the right of the line from (t) to Xmax, and to the left of the line from (t) to (t-1).

Notice that regions 1 or 4 may not exist at a given iteration. The algorithm begins by pushing a "dummy" vertex and Xmin onto the stack. The dummy is placed directly below Xmin, on the line x=Xmin. The algorithm then proceeds as follows:

If the next vertex, t+1, is in (1), ignore it, go to the next vertex.

If t+1 is in (2), delete (t) until (u,t,t+1) form a right turn. Push t+1 onto the stack.

If t+1 is in (3), push it onto the stack.

If t+1 is in (4), ignore it, go to the next vertex.