ElGindy, Avis & Toussaint 1983

ElGindy, Avis and Toussaint presented an algorithm [10] which constructed a weakly externally visible polygon and then applied the Sklansky scan, which is known to work for such polygons (see Sklansky 1972 section).

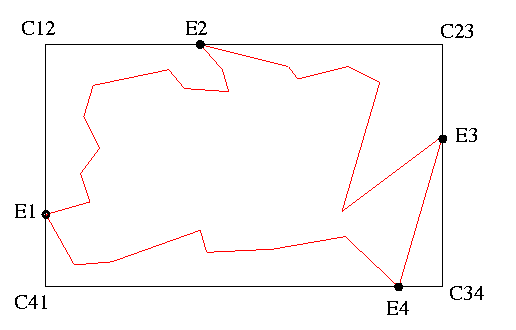
First, the authors find the extreme vertices in the horizontal and vertical directions, and then label the corners of the orthogonal rectangle defined by the extreme vertices as shown below:

For each region inside the rectangle but outside the polygon, a series of steps is applied. I will outline the procedure for the region associated with C12. This region is a simple polygon with vertices E1, C12, E2, Right-chain(E2,E1), where Right-chain denotes the chain of vertices from E2 to E1 that has the original polygon to its left:

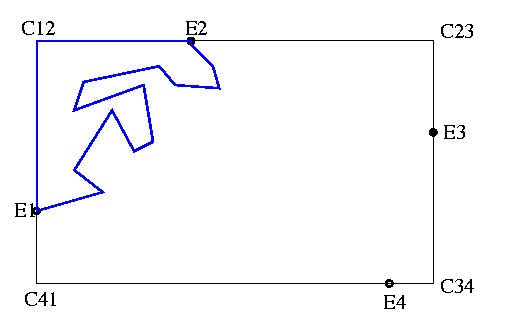
The authors first apply the algorithm VIS-POL of ElGindy and Avis [11], which constructs the visibility polygon from C12. The complexity of this algorithm is O(n). The visibility polygon from C12 is illustrated below in red. Any point of the region that can be joined to C12 with a line segment S, where S is in the interior of the polygon, is part of the visibility polygon.

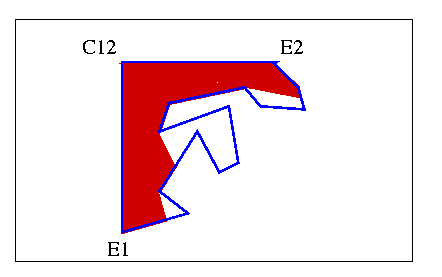
Notice that E1 and E2 must be on the visibility polygon. Also, any vertex of the visibility polygon is either one of the original vertices, or is on one of the original edges, so no new vertices are outside the convex hull of the original polygon. Finally, each new vertex is created from the extension of a line through C12 and an original vertex, so there are O(n) new vertices. Therefore the visibility polygon has O(n) vertices. We can keep the chain from E1 to E2, which is by definition visible from C12 and therefore weakly externally visible.

The next step is to concatenate all such chains and apply the Sklansky scan to the resulting weakly externally visible polygon.

The figure below shows the visibility polygon formed from each corner.

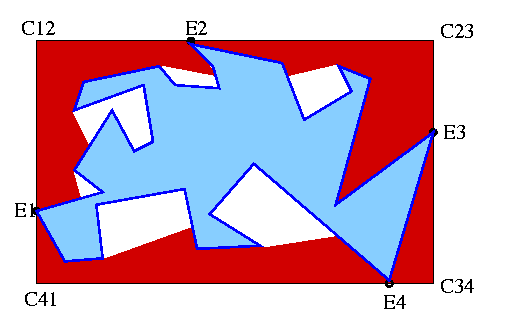
The figure below shows the resulting WEV polygon, where each chain is visible from a corner of the rectangle.