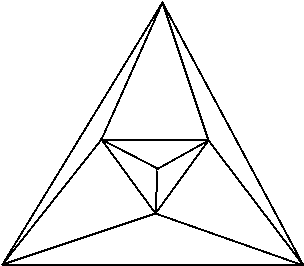
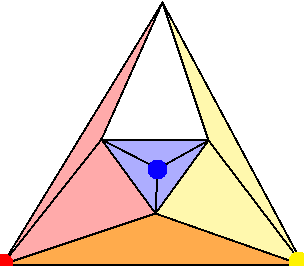
First we look at the lower bounds for placing vertex guards on a polyhedral terrain such that they cover the whole terrain.
Claim: floor(n/2) vertex guards are sufficient to cover any polyhedral terrain.
Proof: We can prove this by a simple four-colouring argument, as in the art gallery theorem (which used a three-colouring argument). If we four color the vertices - this can be done because we can find an equivalent planar graph for our terrain -, we can find two colors such that the number of vertices coloured by these two colors is at most floor(n/2), by the pigeon hole principle.
Let us look at a terrain which actually requires floor(n/2) guards.
The graph shown in Fig. 1 cannot be covered with less than 3 vertex guards, and at most one of them can be on the exterior. This is easily seen from the symmetry of the figure, and because placement of two guards on one of the three exterior vertices will result in an inner triangle (not on the border) being unguarded.


From this basic figure, we can build a sequence of terrains with 4k + 3 vertices requiring 2k + 1 guards, in other words requiring floor( (4k + 3)/2 ) guards.
We can see that we can take the graph in Fig. 1 and construct a smaller version of it within one of its inner triangles. By using a simple inductive proof, we can show that a graph constructed in such a manner k times will have 4k + 3 vertices and will require 2k + 1 guards, because it can have at most one guard on its exterior vertices for it to use the minimum amount of guards.
We will construct a polyhedral terrain T such that T requires floor((4n-4)/13) edge guards to be completely covered.
First let us look at the following graph (Fig.2) which requires at least 2 edge guards, hence exactly achieving the n/3 lower bound.
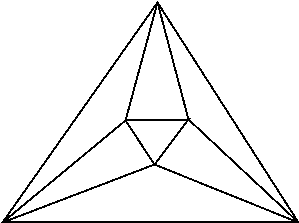
Now from any triangulated convex polygon we can build a planar graph such that this graph will require floor((4n-4)/13) edge guards. Indeed, if this polygon has v vertices (which give v - 2 faces, all triangles) then placing a copy of Fig. 2 in each of the faces and on each of the boundaries give us 2v - 2 such graphs, all requiring 2 guards. We get v + 6*(2v - 2) = 13v - 12 vertices and 4v - 4 edge guards. Then if n = (13v - 12) we can see that we need (4n - 4)/13 edge guards.
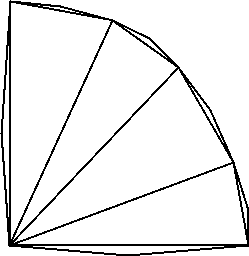
We can construct a terrain based on this graph and so produce a terrain that requires (4n - 4)/13 edge guards to be completely covered. First notice that as for the vertex guards proof, we can construct a terrain whose planar graph is the one shown in Fig. 2. Secondly, we can build a fan-shaped polygon as in Fig. 3 that represents a simple convex terrain. Placing a copy of a terrain based on Fig. 2 on each face of the terrain, we get a n-vertex terrain that requires floor((4n-4)/13).
As a last note, it is important to see that this construction has not reached the floor(n/3) lower bound in terms of edge guards. This gap exists if we attempt to build a convex terrain with the following property; if we simply take any planar graph (such as a set of disconnected triangles), then obviously we can achieve the floor(n/3) lower bound.