Art Gallery Theorems

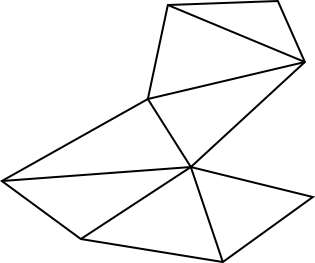
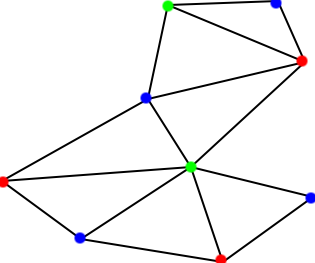
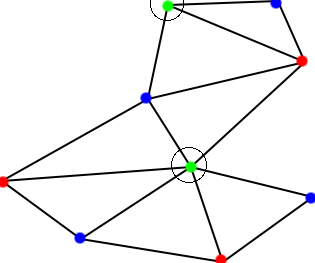
The basic art gallery problem goes as follows. Given a n-sided art gallery - which we reduce to a simple polygon -, we are interested in placing guards at certain points within the polygon such that together they see (guard) the whole polygon. Chvátal, and at a later point Fisk, proved that floor(n/3) guards are always sufficient and sometimes necessary to cover the entire polygon. This can be seen through the following argument, due to Fisk:

1. Take the polygon to be guarded.
2. Triangulate it, which we known can be done for any simple polygon.
3. 3-color the vertices, which can always be done for a triangulated polygon.
4. Pick the smallest set of vertices with the same color and put guards on these. Since there can be at most one vertex of each color on a triangle, then the total number of guards cannot be greater than n/3. Therefore we have found a placement of guards that does not use more than n/3 guards.

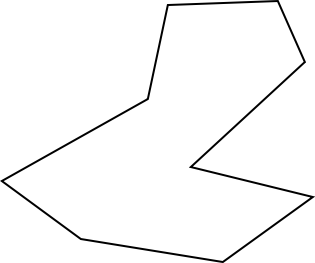
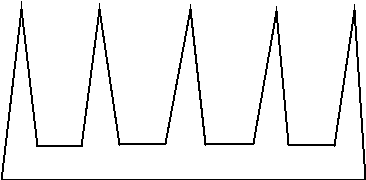
The first part of the theorem, always sufficient, gives the lower bound and is proven in a rough form above; sometimes necessary can be shown by creating a n-sided polygon which needs the said floor(n/3) guards, as the one below.

This subject has been extensively researched, and a linear time algorithm has been found that achieves the lower bound. However, objects in three dimensions have been less studied. Actually, it has been shown that finding the optimal placement (the one that results in the least number of guards being placed) is a NP-complete problem (Cole and Sharir).