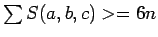 , as we have 10 combinations of colors from
our five coloring. Indeed, each color appears exactly 6 times in the list
of combinations. Now, if
, as we have 10 combinations of colors from
our five coloring. Indeed, each color appears exactly 6 times in the list
of combinations. Now, if 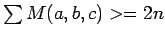 , then we have that the average
G(a,b,c) is
, then we have that the average
G(a,b,c) is
First, it is important to notice that the proof of the floor(n/2) bound on the required number of vertex guards for a convex terrain depends on four coloring the surface's vertices. As such, we cannot directly apply this idea to place guards, since four coloring is NP-complete. However, five coloring is not, and in this section we will see how to use this algorithm in order to place vertex guards.
One simple algorithm that we can use to place vertex guards is as follows. It is based on the idea that if we five-color the vertices of a terrain, then each face to be covered is a triangle and therefore is seen by three differently colored vertices. Then if we take any set of three colors, since there are only five colors in the vertex coloring, at least one of them must be used in each face's vertices. This gives the following simple algorithm:
The proof of the above algorithm goes as follows. First observe that if we take a maximal matching for some color combination, then not all triangles might be guarded by this matching. However, if we add one edge guard for each of the remaining unguarded triangles, then we will cover the whole terrain. If a,b,c are the three colors in question, G(a,b,c) the total size of the set of guards, S(a,b,c) the set of vertices of one of these colors and M(a,b,c) the size of the matching, then we have
Simply because for each edge that we guard, we effectively guard two different colors. Therefore, if we were to use only vertex guards, we would require S(a,b,c) guards, but for each edge guard used, we can take away two vertex guards.
Notice that 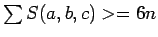 , as we have 10 combinations of colors from
our five coloring. Indeed, each color appears exactly 6 times in the list
of combinations. Now, if
, as we have 10 combinations of colors from
our five coloring. Indeed, each color appears exactly 6 times in the list
of combinations. Now, if 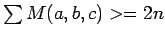 , then we have that the average
G(a,b,c) is
, then we have that the average
G(a,b,c) is
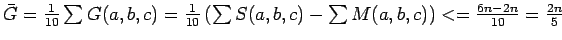
Since there must be at least one set G(a,b,c) such that G(a,b,c) is smaller than the average G(a',b',c') then we know that picking this set will yield a set of guards covering the entire graph (and by extension, the terrain) with size at most floor(2n/5).
If 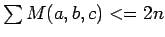 , then we claim that if the colors are named 1..5,
then a pair of matchings from the following list is sufficient to guard
the terrain: { M(1,2,3) and M(1,4,5), M(1,2,5) and M(2,3,4), M(1,2,4) and
M(3,4,5), M(1,3,4) and M(2,3,5), M(1,3,5) and M(2,4,5) }. Without loss
of generality, suppose we pick the first pair, M(1,2,3) and M(1,4,5). Then
suppose there is a triangle that is not guarded. This triangle cannot contain
an edge colored (1,2), (1,3), (2,3), (1,4), (1,5) or (4,5), since it would
be part of the matching as none of the vertices of the triangle are guarded.
So one of the edges must be (2,4), (2,5), (3,4) or (3,5). Therefore the
third vertex of the triangle must be 1, 3, or 5 depending on this edge. But
in all cases, we find that this implies we have two unmatched vertices that
should be in M(1,2,3) or M(1,4,5)! Hence all triangles must be guarded. By
contradiction, we have shown that one of the above pairs of matchings is
sufficient to cover the terrain.
, then we claim that if the colors are named 1..5,
then a pair of matchings from the following list is sufficient to guard
the terrain: { M(1,2,3) and M(1,4,5), M(1,2,5) and M(2,3,4), M(1,2,4) and
M(3,4,5), M(1,3,4) and M(2,3,5), M(1,3,5) and M(2,4,5) }. Without loss
of generality, suppose we pick the first pair, M(1,2,3) and M(1,4,5). Then
suppose there is a triangle that is not guarded. This triangle cannot contain
an edge colored (1,2), (1,3), (2,3), (1,4), (1,5) or (4,5), since it would
be part of the matching as none of the vertices of the triangle are guarded.
So one of the edges must be (2,4), (2,5), (3,4) or (3,5). Therefore the
third vertex of the triangle must be 1, 3, or 5 depending on this edge. But
in all cases, we find that this implies we have two unmatched vertices that
should be in M(1,2,3) or M(1,4,5)! Hence all triangles must be guarded. By
contradiction, we have shown that one of the above pairs of matchings is
sufficient to cover the terrain.
Now, the average size of these pairs is 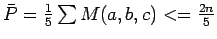 , and thus as
noted above, there must be a pair that has size at most floor(2n/5). It
follows that our algorithm can always find a set of edges (or edges and
vertices) such that floor(2n/5) edge guards are sufficient to cover the
entire terrain. Th algorithm takes O(n) time, since there is a fixed number
of matchings, each taking O(n) time to be found, and five-coloring is O(n).
, and thus as
noted above, there must be a pair that has size at most floor(2n/5). It
follows that our algorithm can always find a set of edges (or edges and
vertices) such that floor(2n/5) edge guards are sufficient to cover the
entire terrain. Th algorithm takes O(n) time, since there is a fixed number
of matchings, each taking O(n) time to be found, and five-coloring is O(n).