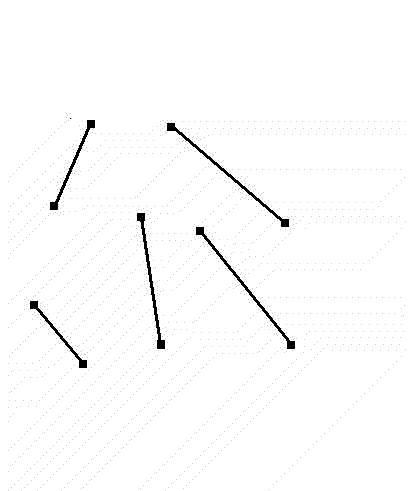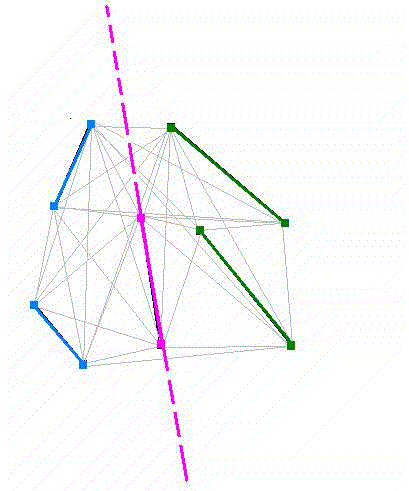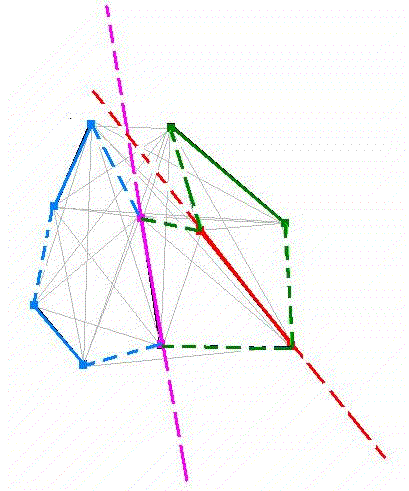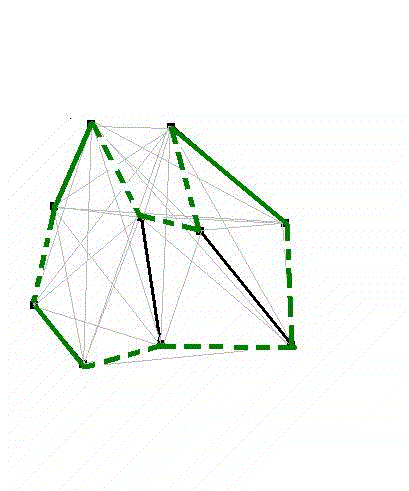
This theorem is proven by induction on the number of segments, n, in the set S.
Base Case:
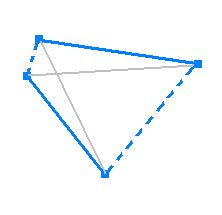
If n = 2. Both segments must lie on the convex hull of S because they are independent, and therefore we just follow the convex hull of S and we get our Hamiltonian Cycle, C.
Induction Hypothesis:
Assume the theorem holds for n = 3,4,....k - 1 segments
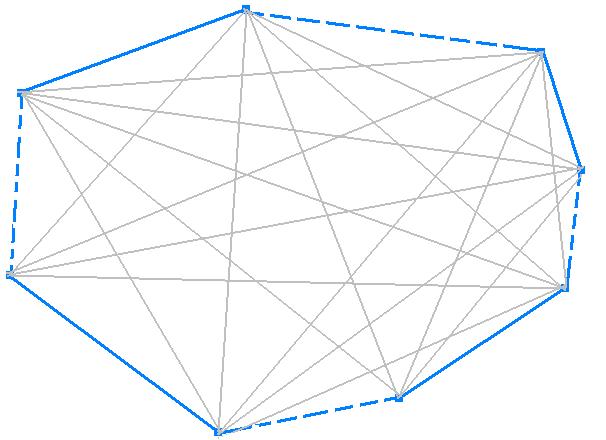
Consider a set S of n=k independent segments
From the n independent segments we choose a segment s, not on the convex hull of S. If there is no such s, than all segments are on the convex hull and once again we may just follow the convex hull of S and we get our Hamiltonian Cycle, C.
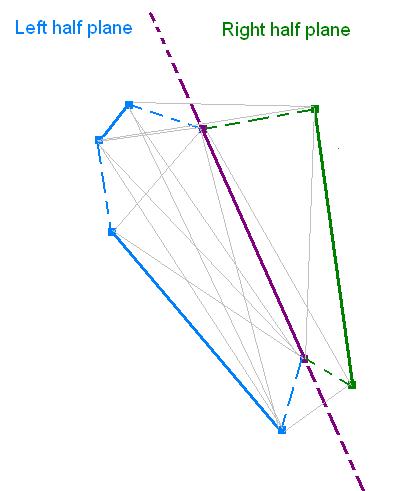
Otherwise arbitrarily choose one such s and divide the set S into two subsets:
L = the segment s, and all segments to the left of s
R = the segment s, and all segments to the right of s.
Since s is not on the convex hull of S it must have segments on either side of it, so the sets L and R both contain at least 2 segments each. Assume that L contains 1<a<k segments, so R would contain k-a+1 segments, where 1<k-a+1<k.
So we can apply the induction hypothesis on both and L and R to get that both subsets contain the desired Hamiltonian Cycles. Furthermore both of these cycles contain both vertices of the segment s, so we simply remove s from each cycle and paste the remainder of our cycles together to get the desired cycle for our set S. QED