Sliding Coins Problems
by:
François Poirier
The sliding coins problem can be a very vague, but very interesting problem. Given a set
of coins of varying size in non-overlapping position, a set of destinations and an agenda
for every coin, or which destinations they are allowed to go to, we are required to find
an itinerary that will satisfy each coin's agenda by moving one coin at a time. Legal
moves are limited to translations, and a coin may not collide with any other coins. We
measure the efficiency of the solution by the number of moves rather than by the distance
the coins travel.
This allows for easy solutions to problems where we do not bound the space the coins can
travel in, as it becomes possible to move coins to infinity in order to save on the number
of moves. For this reason, and because of the amount of problems related to moving coins,
this web page will focus on the following problem: Given n coins and n destinations, with
each coin having a single destination as its agenda, is it possible to find an itinerary
of cost n?
This specific problem would also find the shortest itinerary possible if the problem can
be solved, as an itinerary of cost n means we move each coin only once, so it travels the
shortest distance between its start and destination point. In order to tie the problem with
real-life situations, we can also be think of it as trying to move robots in a room.
Given such a problem, where do we start in solving it? Well, there are a few obvious
observations that could allows us to rule the problem as being impossible to solve. If
two destinations overlap, then one of the two coins will never be able to reach its
destination, so the problem is unsolvable. Also, the same principle applies if two coins
share the same destination.
What if the problem isn't so trivial? It helps to remember that in order to respect the
bound of n moves, each coin can only move once. Therefore, the only legal move each coin
can make is to go straight to its destination. This makes the problem easier to
conceptualize, as we simply have to find an ordering of the possible moves. An example is
shown in figure 1.

Figure 1: A possible configuration for our decision problem
Of course, simply trying every possible combination of moves wouldn't be very efficient.
Another key observation to be made is that only the start and destination positions of
every coin can hamper the progress of other coins. Since we move the coins one by one with
only one move per coin, each coin will either be at its start or destination points at
all time. Therefore, we can attempt to use this information in order to develop an
algorithm to solve the problem efficiently.
Our algorithm does in fact use this observation. The first step in the algorithm is to
construct a structure representing the movement path of each disc, as seen in figure 2.
This is done by connecting the start and destination position via two tangent lines. The
resulting construction is akin to a racetrack, or hippodrome. It should also be noted that
it consists of the same shape as we would get by selecting each point with distance r from
the line segment between the start and end point of the coin, with r being the coin's
radius. The similarity can be seen in figure 3.
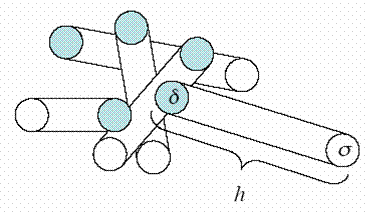
Figure 2: The construction we get from the start and end points
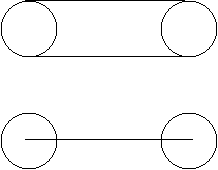
Figure 3: Another way of seeing the hippodrome
It is easy to see that anything that would overlap the hippodromes we built would prevent
the respective coin from moving along its path. This is exactly what we will use them for:
we will create a priority graph that will tell us which coin needs to move first. For
every hippodrome, we will note the positions that overlap with it. We can create the graph
using two simple rules:
If coin i's start position intersects with coin j's hippodrome, we will add an edge from i to j.
This represents that coin i must move before coin j, as coin j cannot move as long as coin
i is in its starting spot.
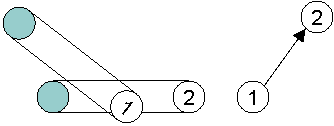
Figure 4: Start position intersecting with a hippodrome
If coin i's destination overlaps coin j's hippodrome, we will add an edge from j to i.
This illustrates that coin j must move before coin i, because if coin i moves first it
will block coin j, which will be left unable to move.
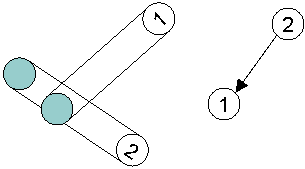
Figure 5: Destination intersecting with a hippodrome
Everything now comes together with the introduction of the following theorem: An itinerary
of cost n exists if there are no directed cycles in the graph we just built. We will prove
the theorem later, but right now we will finish exposing the algorithm.
Thanks to this theorem, we can determine if the problem is solvable by using the graph we
just built. If it isn't, our work is done. If it is, we must find an itinerary satisfying
the target cost. Once again, the graph will again be indispensable to us. We can find an
itinerary by looking at every vertex of the graph and first moving the coins that have no
incoming edges. These coins do not have to wait for others to move out of the way. Once
this is done, we remove those vertices and their edges from the graph, which will make a
few more coins eligible for movement. We keep on repeating this until all coins have been
moved.
The proof of the theorem is actually quite simple. We will begin by assuming there are no
cycles in our graph. Applying our algorithm, we will move the coins represented by
vertices with no incoming edges. Afterwards, we remove these vertices and their edges.
Since there are no cycles in the graph, we are guaranteed that there will be at least one
vertex with no incoming edges, as a graph with no cycles can be rearranged as a tree, and
a tree always has a root which has no incoming edges. We repeat this process until there
are no coins left, so we will have found a complete itinerary.
On the other hand, what do we do when there are cycles in the graph? Quite simply, cycles
indicate contradictions that make the problem impossible to solve. Suggesting that coin a
should move before coin b, which has to move before coin a, is akin to proposing something
like a>b and b>a, which reduces to a>a. This is obviously impossible.
In order to make the algorithm easier to understand, a few examples are given before the
applet. The first example shows a solvable configuration, and the second example shows a n
unsolvable configuration.
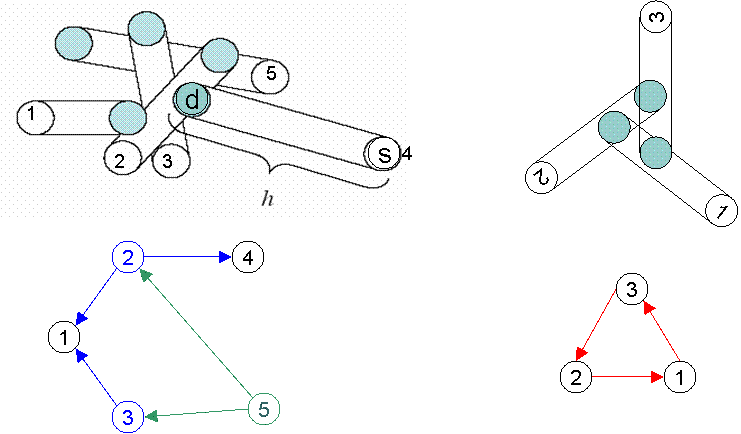
Figure 6: Examples of the application of the algorithm
The following is a Java based applet that allows you to construct a problem and ask the
algorithm to solve it. It enforces the non-overlapping start and finish points. It also
supports various point sizes. The coins are displayed in green (they are at the start
points first), and the destination points are in blue. In order to input points, simply
click the mouse button to place the start point, then hold it and drag the mouse to move
that coin's destination. Release the button when ready to place the destination.
The algorithm has two solving modes: quick and step by step. The quick mode will simply
present an answer, which can then be demonstrated by the step by step mode if the
itinerary is possible. If it isn't, the conflicting coins will be highlighted in red. The
step by step mode can be used to see exactly what the outcome of every point comparison
is. All relevant messages are displayed at the bottom.
1. M. Abellanas, F. Hurtado, A. Garcia Olaverri, D. Rappaport, and J. Tejel. Moving Coins. Japan Conference on Discrete and Computational Geometry, 2004.
2. D. Sunday. About Lines and
Distance of a Point to a Line (2D & 3D).






