The Minimum Width Feasible Annulus Lemma
The Minimum Width Feasible Annulus Lemma (Lemma 5 from "Computing Constrained Minimum-Width Annuli of Point Sets") states that the minimum width feasible annulus with fixed inner radius (covering a specified point set) must have at least:
- Three Points or a Diametral Pair on the Outer Circle;
- Two Points on the Inner Circle and One on the Outer; or
- Two Points on the Outer and One Point on the Inner.
The proof of this is best seen by considering case by case annuli that do not meet the criteria.
In all cases it is possible to transform the annulus so that it has a smaller width.
I will enumerate the various cases and show how the annulus can be made smaller.
It is enough to show that an annulus can be transformed into a smalled width annulus.
It is not necessary to show that the transformed annulus is minimal width.
In fact the transformed annulus is probably not minimum width.
The possible cases are:
- an outer circle that does not contain any points;
- an outer circle that does not contain a single point and an inner circle that contains no points;
- an outer circle that contains a non-diametral pair and an inner circle that contains no points; or
- an outer circle that contains a single point and an inner circle that contains a single point and
- the inner circle can move towards the point on the outer circle, or
- the inner circle can not move towards the point on the outer circle
Example Figures
To illustrate how annuli that meet the various cases can be shrunk, I will use animated figures.
In each figure there is an annulus that covers a point set.
The annulus is in light blue.
The two circles that define the annulus are in dark blue.
The point set that the annulus covers are red dots.
Any reference marks (for example lines to show the direction of movement) are green.
The annulus starts out meeting one of the above cases, but is shrunk.
For reference, the original inner and outer circles are shown (dotted).
The Outer Circle Does Not Contain Any Points
This is probably the easiest case to prove.
Figure 1 shows how an annulus where the outer circle does not contain any points can be shrunk.
Since the outer circle does not contain any points, it must be possible to shrink it (at least a little bit).
Green arrows show the shrinkage.
Clearly the annulus has shrunk.
In all other cases, the technique will be to transform the annulus into an annulus where the outer circle does not contain any points and then apply this technique.
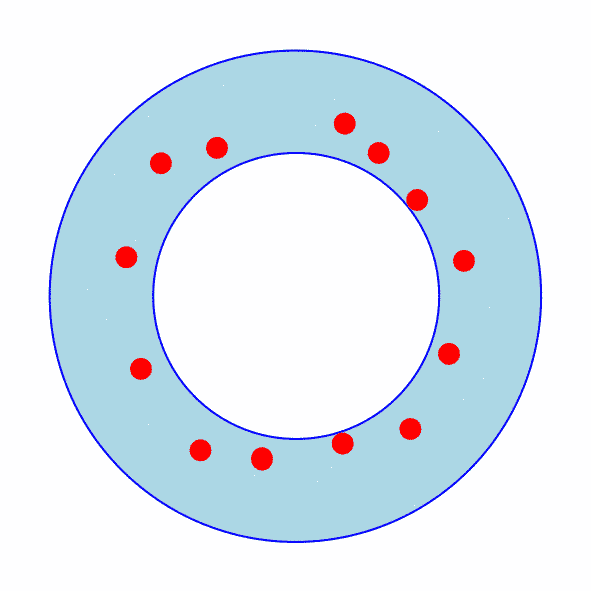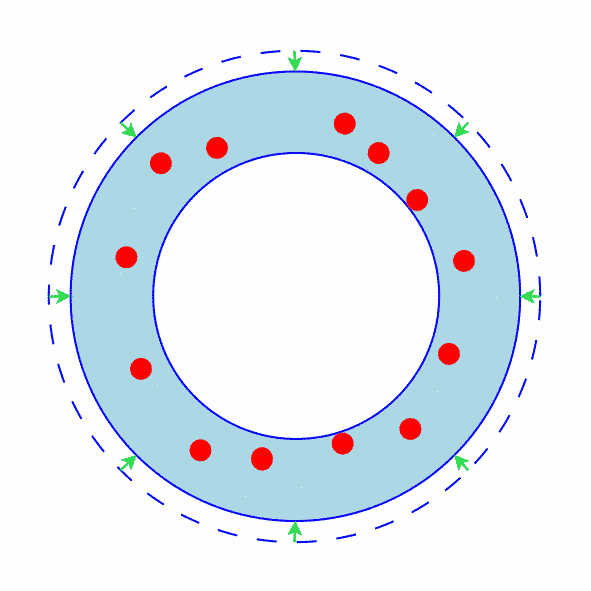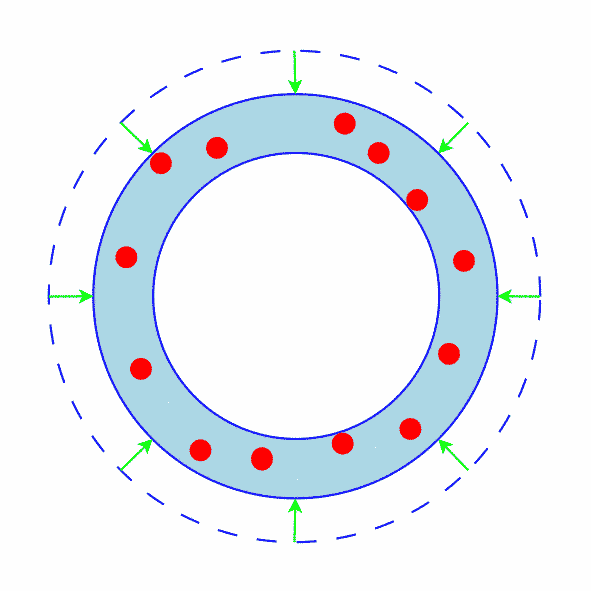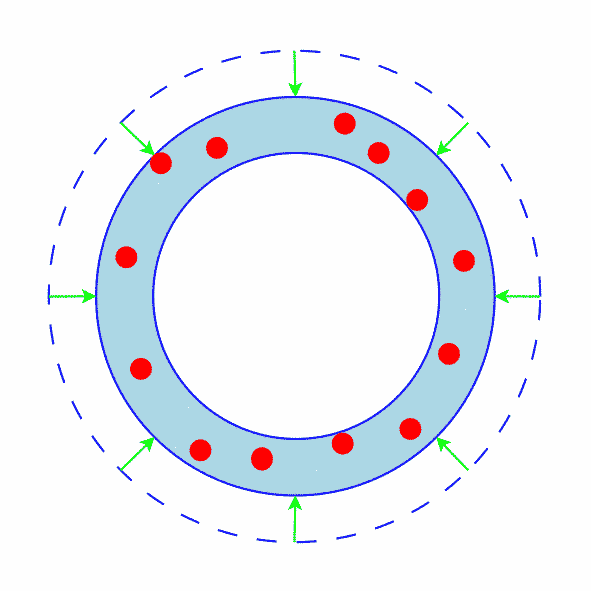 |
Figure 1: The Outer Circle Does Not Contain Any Points
The Outer Circle Contains A Single Point and the Inner Circle Contains No Points
Figure 2 shows how an annulus where the outer circle contains a single point and the inner circle containing no points can be shrunk.
-
Since the inner circle does not contain any points and the outer circle contains just one point, it is possible to move the common center of the annulus (at least a little bit) towards the one point on the outer circle so that neither the inner nor outer circles contain any points.
The direction of movement is depicted with a green arrow.
-
Of course, just moving the annulus does not shrink it, but since the outer circle contains no points, the same procedure applied to the first case can shrink the annulus.
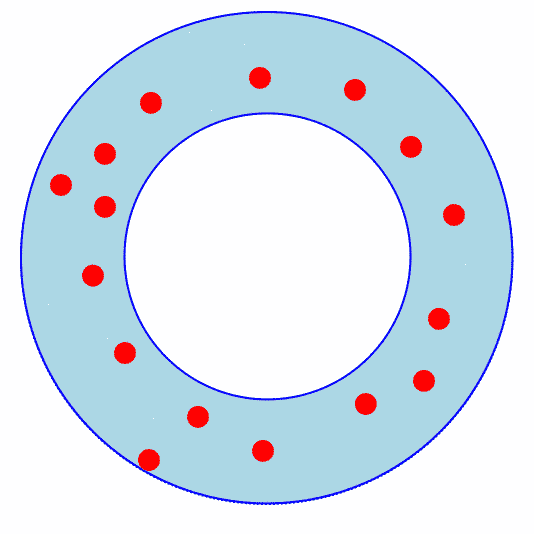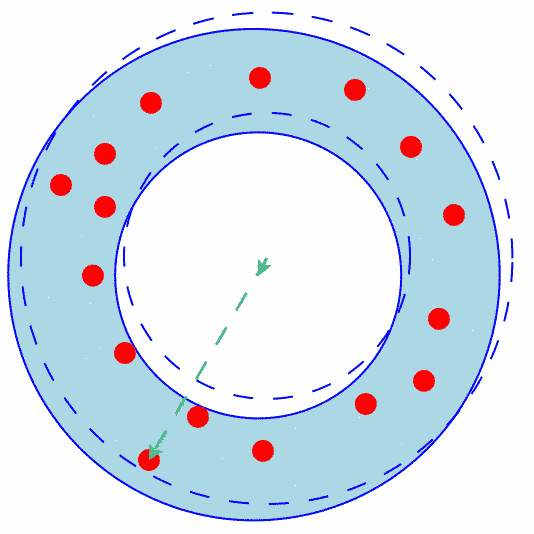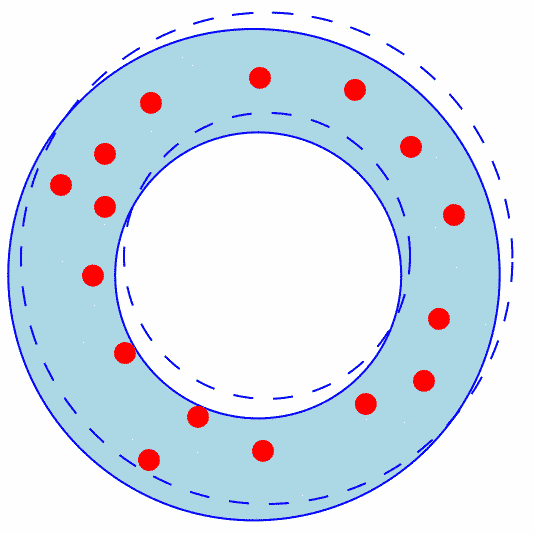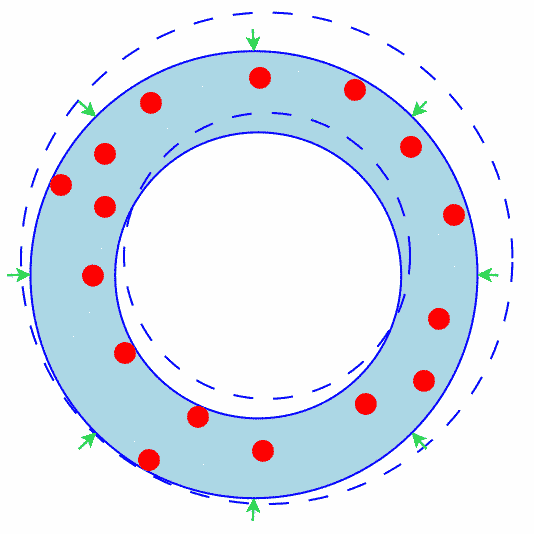 |
Figure 2: The Outer Circle Contains a Single Point and the Inner Circle Contains No Points
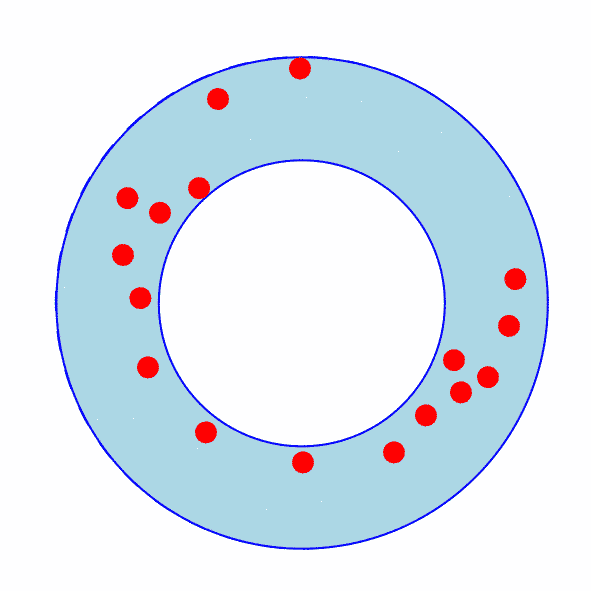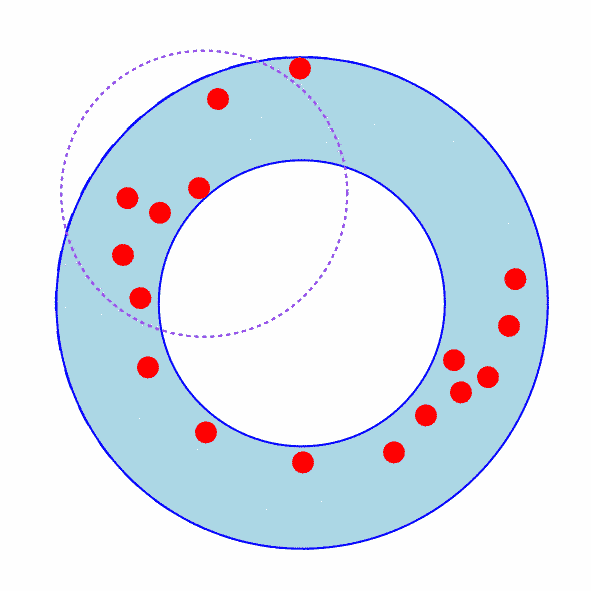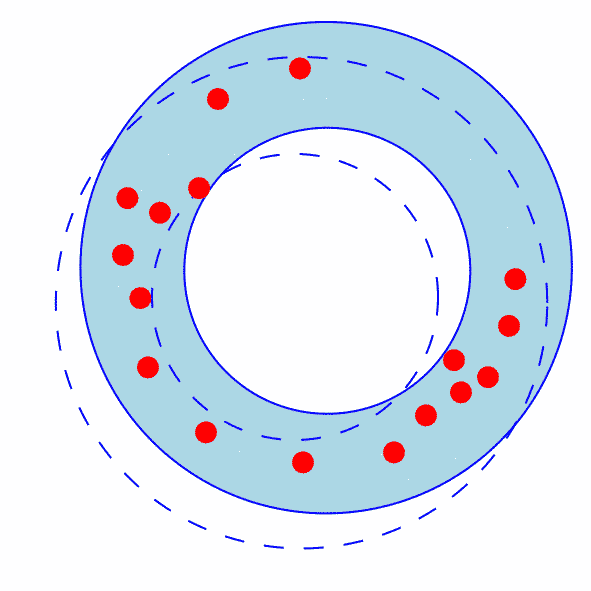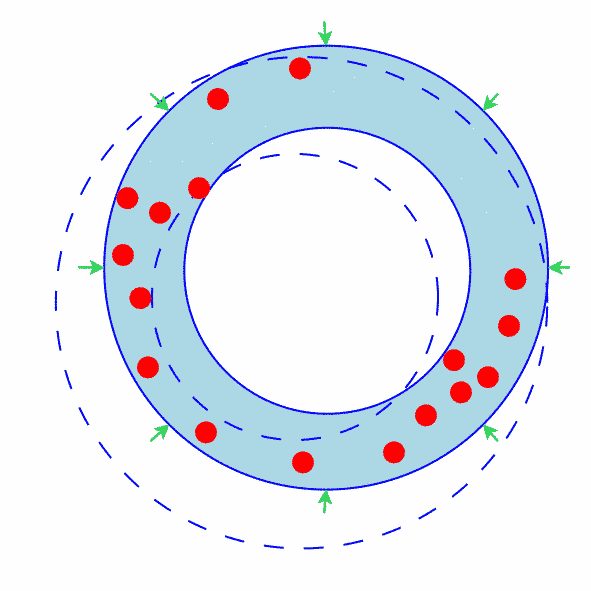
The Outer Circle Contains A Non-Diametral Pair and the Inner Circle Contains No Points
Figure 3 shows how an annulus where the outer circle contains a non-diametral pair (and neither the outer nor inner circles contain any other points) can be shrunk.
The procedure is very similar to the previous case.
However instead of moving the annulus towards a point on the outer circle, move the annulus towards the midpoint of the bisector of the two points on the outer circle.
(For reference the bisector and a directional arrow from the common center to the bisector is shown in green.)
|
|
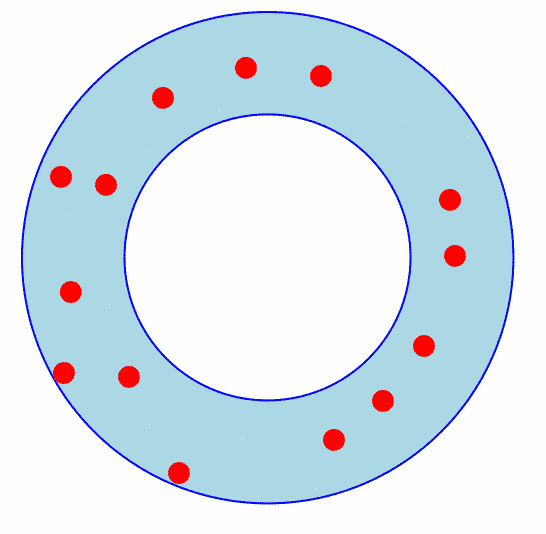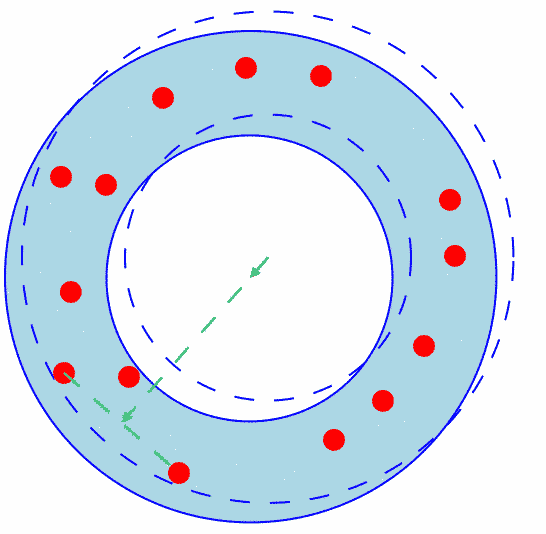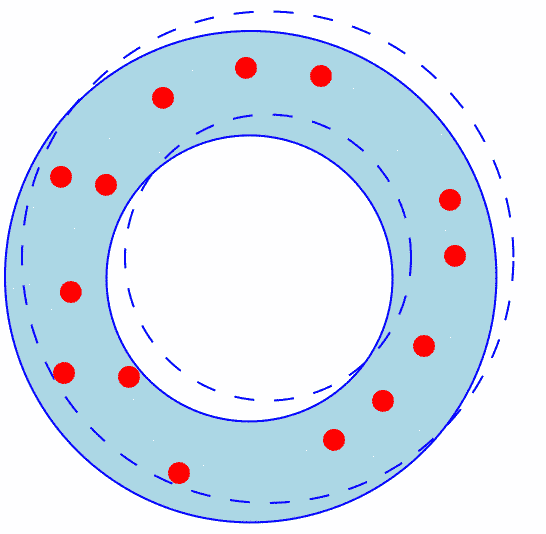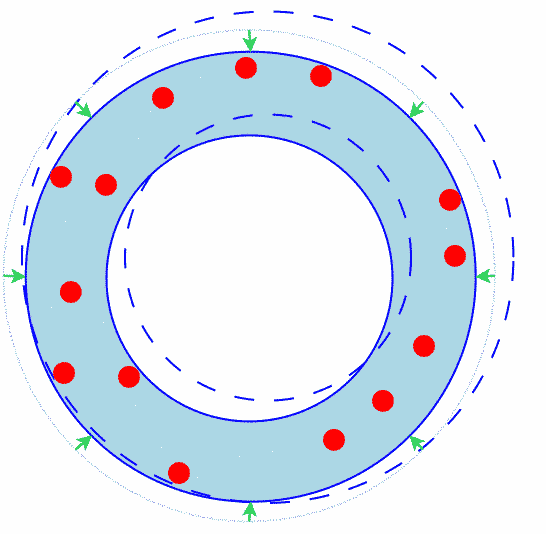 |
Figure 3: The Outer Circle Contains a Non-Diametral Pair and the Inner Circle Contains No Points
The Inner and Outer Circle Contains A Single Point (but the Inner Circle is Free to Move Towards the Point on the Outer Circle)
Figure 4 shows how an annulus where the inner and outer circle both contain a single point (but the inner circle is free to move towards the point on the outer circle) can be shrunk.
The inner circle is free to move towards the point on the outer circle because the point on the inner circle is not in the way.
The procedure is very similar to the second case.
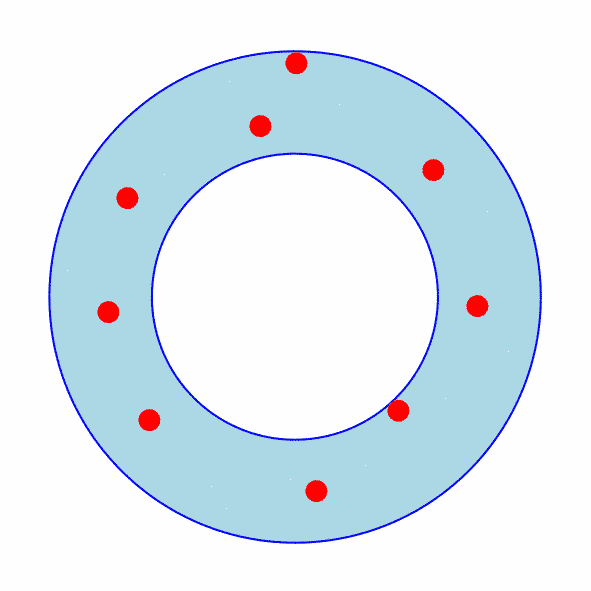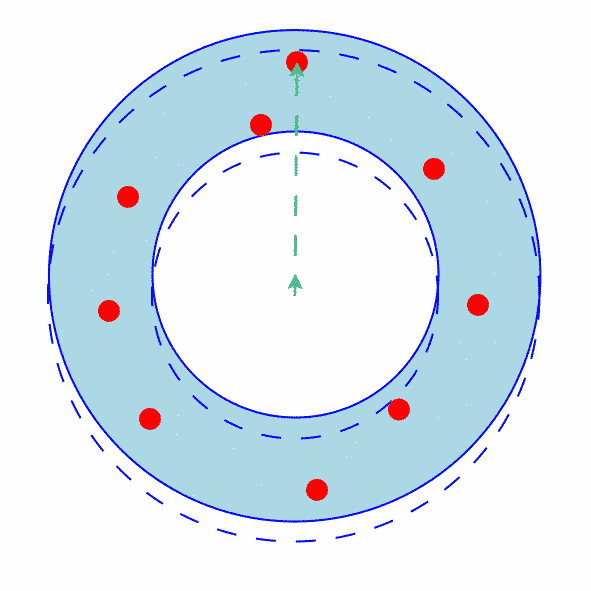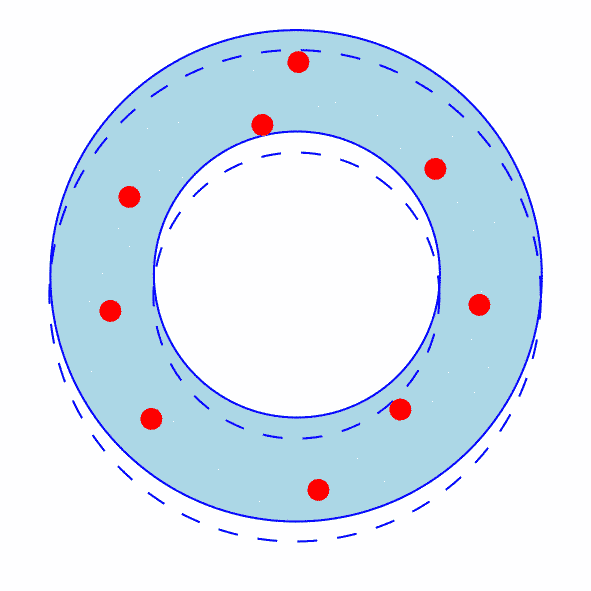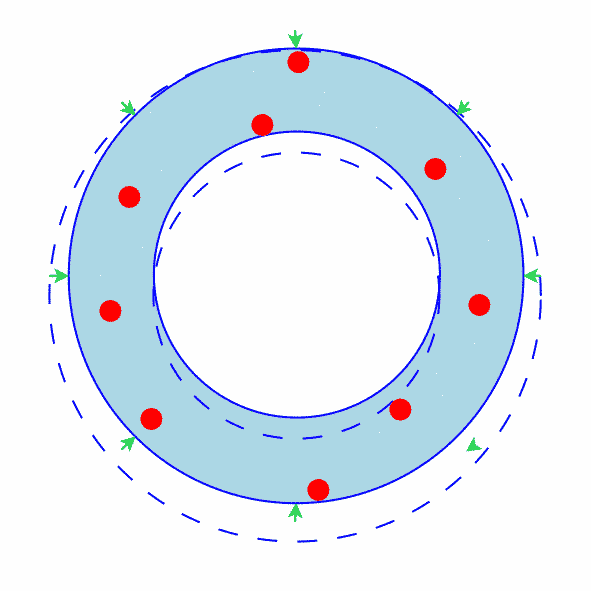 |
Figure 4: The Inner And Outer Circle Contains A Single Point (and the Inner Circle is Free to Move Towards the Point on the Outer Circle)
The Inner and Outer Circle Contains A Single Point (But the Inner Circle is Not Free to Move Towards the Point on the Outer Circle)
This is probably the most difficult case to prove.
Figure 5 shows how an annulus where
- the outer circle contains a single point;
- and the inner circle contains a single point; and
- we can not move the inner circle towards the point on the outer circle (because the inner circle point is in the way).
can be shrunk.
-
Consider a circle that is centered on the point on the inner circle.
(Let's call it the defining circle.)
In the figure, the defining circle is shown in purple.
The defining circle must contain the common center.
-
It must be possible to move the common center along the defining circle to a point that is at least a little bit closer to the point on the outer circle.
After moving the annulus, the inner circle will still contain its point.
But the outer circle will no longer contain any points.
Now the same procedure employed in the first case can be used to shrink the annulus.