The constrained minimum-width annulus of a set of points

Introduction

Annuli Are Doughnuts! (sort of)

Figure 1: A student examines annulus-like shapes

Formally, an annulus is the area bounded by and contained within two concentric circles. This geometric construction is also known as a "doughnut." (However as Figure 1 shows, not all doughnuts are annuli.)

What is a Minimum-Width Annulus?

The width of an annulus is the difference between the radii of its two defining circles. Usually an annulus is covering a set of points. If the annulus is minimum width then

• if we increased the inner radius (reducing the width) then some points would no longer be covered; and
• we decreased the outer radius (also decreasing the width) then again some points would no longer be covered.

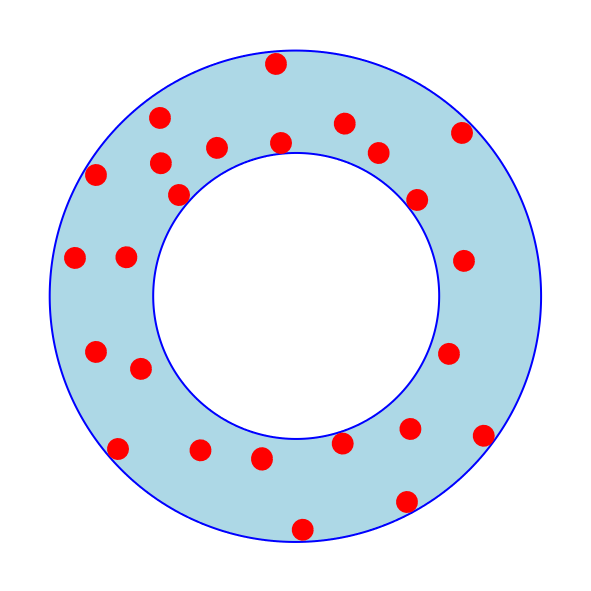
Figure 2 shows an annulus that covers several points. The annulus itself is light blue. As you can see it is defined by two concentric circles - the inner circle and the outer circle. Both the inner and outer circle are shown in dark blue. The points are depicted as red dots. You can think of this annulus as a blueberry doughnut with red sprinkles if you like. This is how this project graphically depicts annuli.

Figure 2: An annulus

I will not try to formally argue that Figure 2 is a minimum width annulus. In this case, it should be obvious from visual inspection. But informally, it should be clear that you can not make the inner circle any bigger nor the outer circle any smaller and still cover the point set. Thus the width of the annulus can not be made smaller.

Variation of the Problem

There are several interesting variations on the minimum-width annulus problem. I will briefly introduce three: the fixed outer radius, the fixed inner radius, and the fixed median radius. However for simplicity throughout the rest of this web tutorial, I will only discuss the fixed inner radius variation. If you are interested in the other variations, then I invite you to read a more advanced reference

In the fixed outer radius variation, the radius of the outer circle is fixed at a specified value. The radius of the inner circle can be as small as a point (for the fattest possible annulus) or as large as the outer circle (for the thinnest possible annulus).

It should be trivial to see that it is sometimes impossible to produce a single annulus that covers a given point set with this restriction. Figure 3 illustrates a point set where it is impossible to produce a single covering annulus (with the specified outer circle radius). As you can see, it does not matter what size the inner circle is. The outer circle simply can not cover all the points.

Figure 3: An Impossible Fixed Outer Radius Minimum Annulus Problem

The Fixed Inner Radius

The fixed inner radius problem is very similar to the fixed outer radius problem except that the radius of the inner circle is fixed. The radius of the outer circle can be as small as the inner circle (for the thinnest possible annulus) and it can be arbitrarily large.

It should be obvious that there will always be at least one annulus that covers a given point set (even with this restriction). One way to find such an annulus starts with putting the inner circle just to the right of the right most point in the point set. Then enlarge the outer circle until it covers the entire point set. (Hint: It should not be necessary to enlarge the radius of the outer circle more than the diameter of the point set in addition.) While this annulus is most likely not minimal, the exercise should convince you that a minimal annulus exists.

Figure 3: A Fixed Inner Circle Radius Minimum Annulus Problem

The Fixed Median Radius

The median circle is a circle with the same center as the inner and outer circle. The median circle lies equidistance from the inner and outer circles. In the fixed median radius problem, the radius of the median circle is fixed. The radii of both the inner and outer circle may vary, but they must vary together. In one extreme (the fattest possible annulus) the inner circle is a single point and the outer circle's radius is twice the median radius. In the other extreme (the thinnest possible annulus) the inner, median, and outer circle all have a common radius.

Figure 5 illustrates the fixed median radius minimum annulus problem. The green dotted circle is the fixed median radius. The diameters of both the inner and outer circles can be adjusted, but they must be adjusted together.

Figure 5: A Fixed Median Radius Minimum Annulus Problem

It is more difficult to visualize this variation than the previous two problems. It is sometimes impossible to produce a single annulus that covers a given point set with this restriction. To see that it might be impossible to produce a single covering annulus, recall that the radius of the outer circle can only be increased so much. Thus if the diameter of the point set is too large then it simply will be impossible to produce a covering annulus. (This is very similar to the fixed outer median radius minimum annulus problem.)