Background and Applications

Metrology is the science of measurement and one of its topics is measuring roundness.

A Square-Wheeled Bicycle? No Way!

While consumers may be open to doughnuts that are not round, roundness can be an important quality of manufactured products. Most consumers would not buy Professor Wagon's square-wheeled bike (pictured in Figure 1).

Figure 1: A Square-Wheeled Bicycle

Measuring the Roundness of an Object

One way to measure the roundness of an object is to measure points from the edge of the object. Commonly the object is rotated while a probe takes measurements. If the object is perfectly round then a zero-width annulus should be able to cover all the measured points. However in the real world no object is perfectly round and no measuring device is without error. If a very small width annulus can cover the measured points, then the object is acceptably round. On the other hand, if the smallest annulus that can cover the measured points is too large, then the object should be rejected as not round enough.

Figure 3 demonstrate a roundness testing of a round object and a non-round "defective" object. First a probe takes measurements from the edge as the object is rotated. Then a minimum width annulus is calculated. Clearly, the defective object needs a bigger annulus to cover the measured points.

Figure 3: Measuring the Roundness of a Round and Square Object

Round Object	Defective Object

Some facilities are highly desirable. Everyone wants schools, libraries, and hospitals to be nearby.

Some other facilities are highly obnoxious. No one wants a prison or garbage dump to be "in their backyard."

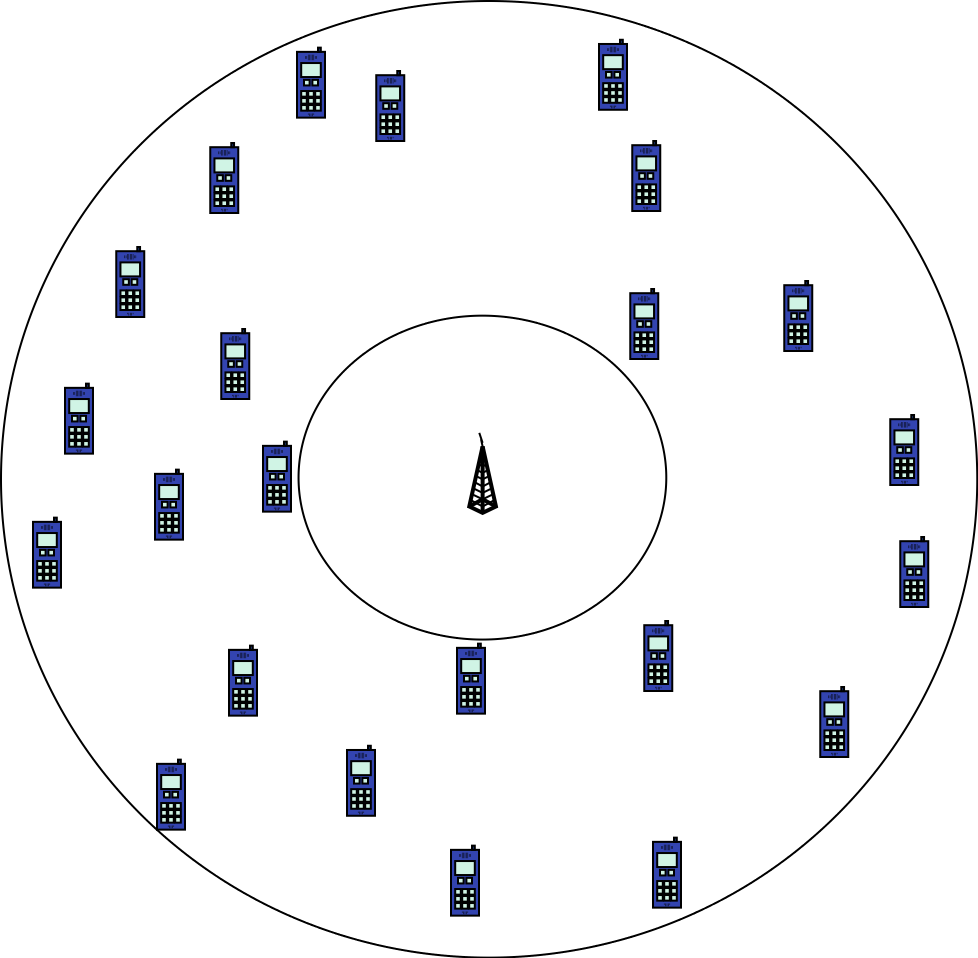
Many facilities have desirable and obnoxious properies. One example is the cell phone tower. Since practically everyone has a cell phone, cell phone towers are needed. However cell phone towers are not appreciated aesthetically (Figure 4) and there may be health concerns from living too close to a cell phone tower.

Figure 4: The crane marks the site of a proposed cell phone tower.

One solution is to construct a minimum width annulus (as illustrated in Figure 5). The outer circle marks the service boundaries of the tower. Place the tower within the inner circle. By finding a minimum width annulus, the tower serves many people but is not too close to anyone.

Figure 5: Illustration of how a minimum width annulus could help locate a cell phone tower.