Introduction

Algorithms in computational geometry are usually designed for the real RAM (random access machine) assuming that the input is in general position.  The general position assumption implies that the input to an algorithm for solving a specific problem is free of certain degeneracies.  There are two kinds of degeneracies:

• Intrinsic (problem-induced). for example, in computing the convex hull, three collinear points is problem-induced degeneracy.
• Extrinsic (algorithm-induced). for certain vertical line-sweep algorithms, two points with the same x-coordinates constitute an algorithm-induced degeneracy.

 Existing methods for removing degeneracies in computational geometry can be classified as either:

• Approximation.
• Perturbation.

• Some Extrinsic degeneracies can in fact be removed by a global rigid transformation. Once the solution is obtained on the transformed non-degenerate input, it can be transformed back trivially to yield the solution to the original problem.

1. no two points(2D) in the plane have the same x-coordinate;
2. no two points(3D) in space lie on a vertical line;
3. no two points in space have the same x-coordinate;
   

Definitions

• Regular projection:
  
• A projection of point set S (n points) on a line L is said to be regular if each point in S projects to a distinct point on L. In other words the project contains n distinct points.
• Let S be a set of n distinct points in Euclidean space and Let H be a plane, a projection of S on H is said to be regular if each point in S projects to a distinct point on H.

• Maximum projective tolerance:
• The projection that allows the greatest angular deviation of the viewpoint without violating the regularity of the projection, i.e,. without creating degeneracies. We call this regular projection with maximum projective tolerance.

Degeneracy 1: no two points in the plane have the same x-coordinate

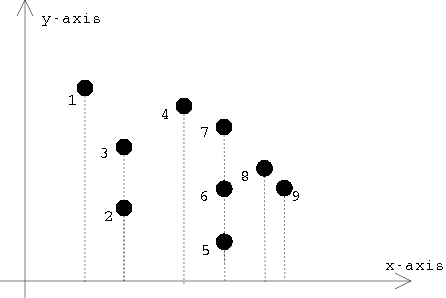
Figure 1: A non-regular projection of points(2D) on the x-axis.

The Decision Problem

A very simple algorithm suffices since we simply need to check for duplicates in the x-coordinate values of the point set S. this can be done in O(n log n) time by sorting these values. The projection is regular if and only if there are no duplicates. The lower bound can be established  by a reduction from the element-uniqueness problem.

Theorem 1.1: Given a set of S of n distinct points in the plane and a line L, whether S admits a regular onto L can be determined in O(n log n) time.

The Computation problem

Given a set S of n distinct points in the plane, find a rotation of S that removes the degeneracies, or equivalently, a line L such that S yields a regular projection on L. A regular projection always existed because the only forbidden directions of projections are those determined by the lines through pairs of points of S, see Figure 2.

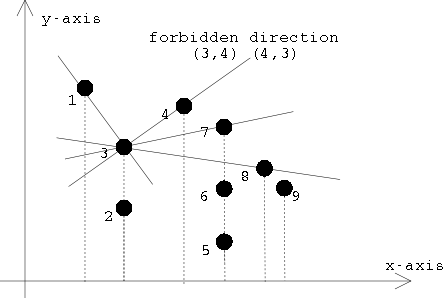
Figure 2: construct the forbidden directions by connecting each pair of points in S

Let the circle C², representing the set of forbidden directions, be the unit circle in the plane, centered at the origin. For every pair of points in S, translate the line through them so that it intersects the origin. Intersect each such line with C² to yield a pair of forbidden points on C².  Altogether there are O(n²) such forbidden points. see Figure 3.

Figure 3:  construct the forbidden points on unit circle.

We may determine a direction for a regular projection by finding a point in the interior of any arc of C² that is bounded by two distinct adjacent forbidden points. Such a point on C² may be found easily in O(n² log n) time by using the brute-force approach of sorting the forbidden points.

A quicker approach is generate a random direction points on C², check if it is conflict with the existing forbidden points, if not, we get the desired rotation scheme. if it does conflict with the existing forbidden points, we regenerate another random points, and continue to check it.  The total excepted run time should be O(n²).

Actually we can get this by O(n log n) time. See Figure 3, let 'a'to be the points with largest slope which lies on y-axis, if we can find the second largest slope (say 'b'), then we can choose any point (say 'c') in the arc between 'a' and 'b'. rotate the y-axis to align with 'c', we can get the regular projection.  how could we find the second largest slope? there is a trick, in fact we don't really compute and find the second largest slope which will take O(n²) time, we just find its upper bound. this is can be done as follows:

1. Find the largest and smallest y-coordinate of the points in S,  we get max_S(delta(y)) = y_max - y_min.  ---  O(n) time.
2. Sort the x-coordinates of the points in S, and discard the duplicates, find the smallest the gap min_S'(delta(x)). ---  O(n log n) time.
3. Compute the upper bound for the Second largest slope:
   

    max_S(delta(y)) / min_S'(delta(x))

Where S' is the distinct projection points of S on x-axis. We can easily see this value is not less than the second largest slope. see Figure 4.

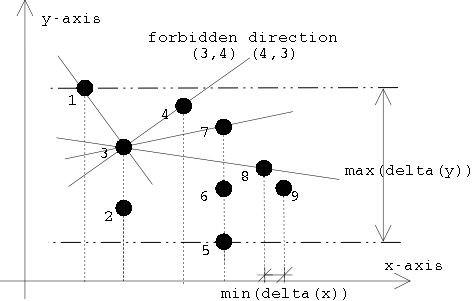
Figure 4: Computing abound on the second largest distinct slope.

Proof:

1. we know the second largest slope = max_S(delta(y)/delta(x)),  when delta(x) != 0.
2. and it is easily to see: max_S(delta(y)/delta(x)) <= max_S(delta(y)) / min_S'(delta(x)).

Theorem 1.2: Given a set of S of n distinct points in the plane, finding a regular projection takes O(n log n) time.

The Optimization Problem

We consider now the question of not merely removing the degeneracies (finding a regular projection), but removing them in the best way possible, say with maximum projective tolerance.

See Figure 3,  we know this question is determined by the mid-point of the largest gap among consecutive forbidden points on C²,  the circle of directions.  The  largest gap can be found by sorting the O(n²) forbidden points.

Theorem 1.3: Given a set of S of n distinct points in the plane, a regular projection with the maximum projective tolerance can be computed in O(n²logn) time and O(n²) space.

Degeneracy 2: no two points in space lie on a vertical line

The Decision Problem

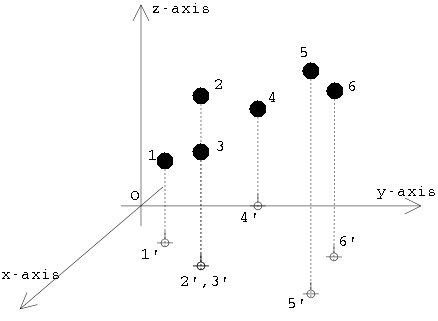
Figure 5: A non-regular projection of points(3D) on the xy-plane.

Let S be a set of n distinct points in Euclidean space and Let H be the xy-plane,  no two points in space lie on a vertical line if each point in S projects to distinct point on H.  See Figure 5: point 2, 3 have same project point on xy-plane. so it isn't a regular projection.

Let S_xy denote the set of points obtained by projecting S onto the H (xy-plane).  First, sort the points in S_xy lexicographically by x and y coordinates.  Scan through the sorted list to determine whether two (or more) points in S_xy have the same x and y coordinates, we can tell whether there are vertical line degeneracies. which takes O(n log n) time.

Theorem 2.1: Given a set of S of n distinct points in space and a plane H, determining whether S admits a regular projection onto H takes O(n log n).

The Computation problem

As in the 2D case, the only forbidden directions of projections are given by line in space going through pairs of points in S, because S does not admit a regular projection onto planes perpendicular to these lines. By translating every such line to origin and intersecting it with the sphere of directions, we obtain O(n²) (not necessarily distinct) forbidden points on C³.

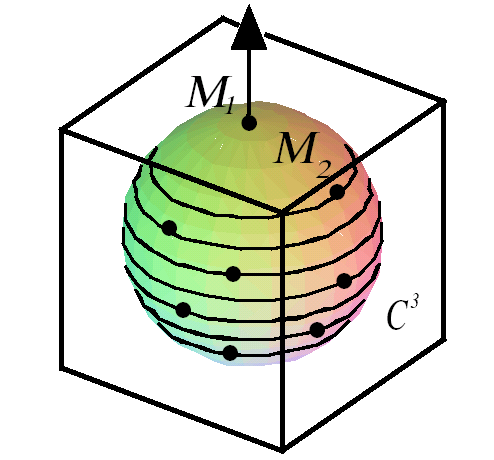
Figure 6: forbidden points on unit sphere and its latitude circle.

if S doesn't project regularly onto the xy-plane, then there is at least one forbidden point at the "north-pole" of the sphere, say it is M₁,  Let M₂  denote the second largest slope point, we know any sphere point in the latitude circle of M₂ except M₁ can yield a regular projection. See Figure 6.

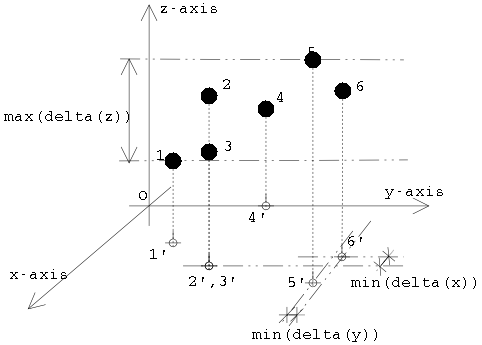
Figure 7: Fast algorithm for upper bound of the second largest slope.

As in 2D case, we will compute the upper bound of the second largest slope, instead of  the second largest slope.  the algorithm follows:

1. Let S_xy, S_x and S_y denote the sets of points obtained by projecting S onto the xy-plane, x-axis and y-axis, respectively.
   
2. Sort each of S_xy, S_x and S_y lexicographically.  --- O(n log n) time.
   
3. Scan through each sorted list to remove multiple occurrences of a point ( keeping one copy). Call these new sorted lists S_xy^*, S_x^* and S_y^*, respectively.
   
4. Compute the width of S in the z-direction.  max_S{delta(z)}. Also compute d = min{min_Sx^*{delta(x)}, min_Sy^*{delta(y)}}.
   
5. The upper bound of the second largest slope M₂ is max_S{delta(z)} / d.
   

The Optimization Problem

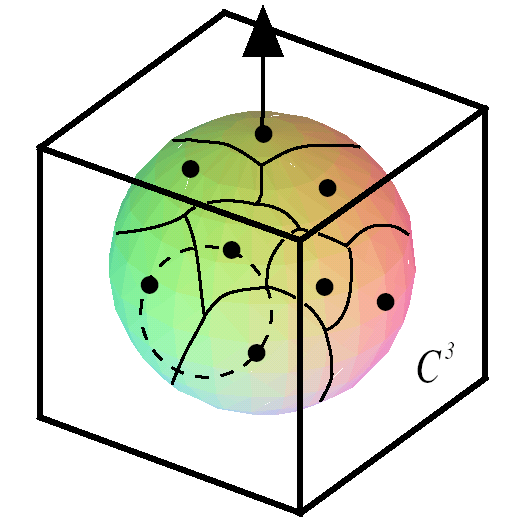
Figure 8: The largest empty circle on the surface of the direction sphere.

It is easily to see that such a direction should be determined by the center of the largest empty circle among the m = O(n²) forbidden points on C³,  See Figure 8.

1. Find and discard all duplicate points on C³ by performing a lexicographic sort of the forbidden points.  ---  O(m log m)
   
2. Computing the convex hull of the points.  ---  O(m log m)
   
3. Computing The Voronoi diagram on the sphere from the convex hull in linearly time.  ---  O(m).  The lower convex hull when projected to the plane is the Delaunay triangulation which is the dual of the Voronoi diagram and can be computed trivially from it.  See Brown[3] for detail.
   
4. get the largest empty circle. O(m).
5. the optimal direction is determined by the center of the empty largest circle.

Theorem 2.3: Given a set of S of n distinct points in space, a regular projection plane with the maximum projective tolerance can be computed in O(n² log n) time and O(n²) space.

Degeneracy 3: no two points in space have the same x-coordinates

The Decision Problem

The Computation problem

The problem is find a line L that S yields a regular projection onto L. This can be done as follows:

1. First find a plane of regular projection for S.  Let H be such a plane and let S_H be the planar set of points obtained by projecting S onto H. ---  O(n log n) time,  Theorem 2.2.
2. In the plane H, find a line of regular projection for SH.  Let L be such a line. Since there are no duplicates in S_H, L is also a line of regular projection for S. --- O(n log n) time, Theorem 1.2.
3. Finally, we can translate and rotate the line L so that it coincides with the x-axis. See Figure 9.
   

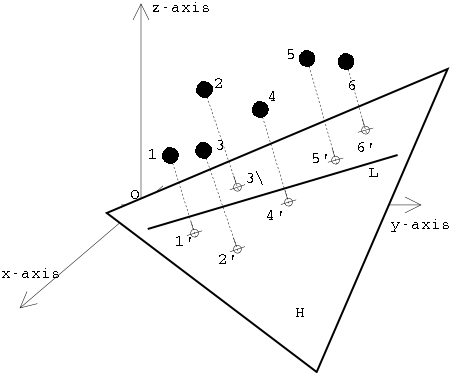
Figure 9: two steps to find a regular projection.

Theorem 3.2: Given a set of S of n distinct points in space,  a rotation of S such that no two points have the same x-coordinate can be computed in O(n log n) time.

This result also can be generalized so that no two points have the same coordinate for two or all three coordinates axes can be computed in O(n log n) time. See Gomez[1] for detail.

The Optimization Problem

See Figure 10, we see for any line, say L', which lies on the  plane H perpendicular to the line ab,  points a and b will have the same projection points on L'.

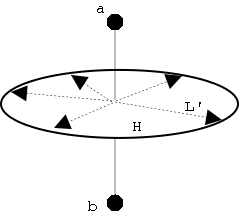
Figure 10: Any projection line lie on the  plane H perpendicular to ab will introduce degeneracy.

Therefore a pair of points in S yields a great circle on the sphere C³ as the set of forbidden directions for the desired x-axis. Thus the entire set S yields an arrangement of O(n²) great circles on C³, See Figure 11.

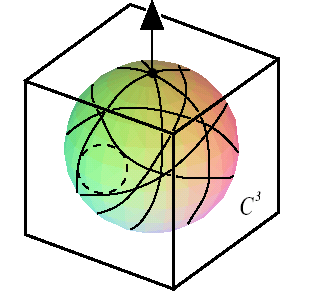
Figure 11: The largest circle contained in a face of the arrangement.

To find a projection of maximum projective tolerance, we need to find a point on the sphere C³ which is the center of the largest spherical disc contained in a face of the arrangement of great circles.

There are O(n²) great circles with a total of O(n⁴) intersections in the arrangement. Compute the entire arrangement and the largest spherical disc contained in each face, which takes time linear in the size of the face. It follows a line L in space such that S yields the regular projection onto L with the maximum projective tolerance can be found in O(n⁴) time and space.

However, this problem could be solved by a different way:

1. As in the Degeneracy 2 case, we compute the forbidden points on the sphere C³ for each pairs points in S. Let S_f denote the forbidden points set.
   
2. We can prove that finding the largest circle contained in the face of the arrangement (See Figure 11) is equivalent to computing the smallest enclosing cylinder containing S_f.  For the proof, see Gomez[1],
3. Computing the smallest enclosing cylinder containing S_f. ---  O(n^3+e), for any e > 0.  Pankakj[2].
   
4. The axes of the smallest enclosing cylinder is the direction with maximum projective tolerance.
   

Theorem 3.3: Given a set of S of n distinct points in space,  a line L in space such that S yields a regular projective onto L with the maximum projective tolerance can be found in O(n^3+e) time and space, for any e > 0.

Applet

Implemented Features:

Keywords

• General Position: The general position assumption implies that the input to an algorithm for solving a specific problem is free of certain degeneracies.
• Lexicographical Sort:  Compare two points first by its x-coordinate, if they is equal, then compare their y-coordinate, an so on z-coordinate. sort by this way, we mean we do lexicographical sort.
  
• Great circle: The plane of great circle passes the center of the sphere.
  

References & Links

1. Francisco Gomez, Suneeta Ramaswami and Godfried T. Toussaint, "On removing non-degeneracy assumptions in computational geometry," Proceedings of the Italian Conference on Algorithms, March 12-14, 1997, Rome, Italy, pp. 52-63.
2. Pankaj K. Agarwal, Boris Aronov, Micha Sharir, "Line Transversals of Balls and Smallest Enclosing Cylinders in Three Dimensions", May 14, 1997.
3. K. Q. Brown. "Geometric transforms for fast geometric algorithms". Ph.D. thesis, Department of Computer Science, Carnegie-Mellon University, Pittsbugh, PA, 1980. Report CMU-CS-80-101.
   
4. J. O'Rourke (1998). Computational Geometry in C (2nd ed.)

Thanks

• Prof. Godfried T. Toussaint is one of the best professors I have met in my life, he taught us a lot very insightful and interesting things. I benefit from him a lot.
• This web page style is "borrowed" from the "3-Coins Algorithm Tutorial (Greg Aloupis and Bohdan Kaluzny)". Thanks to Greg Aloupis and Bohdan Kaluzny.