How Fast is it ?

The algorithm presented here can convexify any monotone polygon in O(n²) moves, each of which take a constant amount of time to compute. We'll start by seeing how we can execute the motion above in a constant amount of time.

Time for Each Move

We simply need to compute which of the five events that could stop the motion will occur first. Recall that the events are:

j₀ straightens,
j₁ straighthens,
j_p-1 straightens,
j_p straightens,
j₀, j₁ and j_p-1 become colinear.

We can note right away that it isn't necessary to check for the second event directly, since the last event, that j₀, j₁ and j_p-1 become colinear, will occur before (or at the same time as) j₁ straightens.

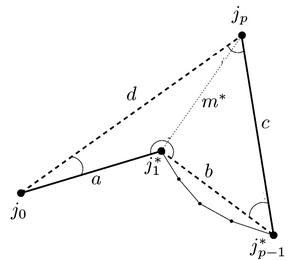
The key to solving this problem is to notice that the distance m from j₁ to j_p always increases during a move. This is almost obvious: j₁ rotates counterclockwise about j₀ while both j₀ and j_p remain at the same position. Also, we showed in the proof of correctness that j₁ always remains in the wedge defined by u and v. Then the angle j_pj₀j₁ always increases, thereby increasing the distance m.

We can use the law of cosines to solve for m in the case of each event, then the stopping event is simply that for which m is the smallest.

Solving the four equations so obtained always takes the same amount of time, so each move takes a constant amount of time. Now we need to see how many moves may be required.

Number of moves required

Let n be the number of joints in the linkage. We've already shown that all the moving joints always approach 180º. Therefore, we will never need to straighten more than n joints, as a straight joint never "un-straightens".

So we just need to determine how many moves it can take to straighten one of the joints.

We only stop a move if a joint has straightened or if j₀, j₁ and j_p-1 become colinear. We've already determined that the first can only occur n times. Now we'll show that the second can only happen up to n-3 times for each straightened reflex joint.

Whenever the three points become colinear, we decrement p and execute another move. In the beginning, p is at most n-1. And we know that p is always at least 3. So we can only decrement it n-3 times for each reflex vertex.

Finally, at most O( n² ) moves are needed, each of which takes a constant amount of time to compute, so the running time of the algorithm is quadratic.