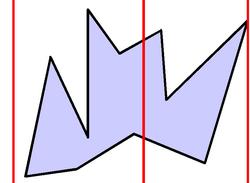
A monotone polygon is a polygon whose intersection with any vertical line is an interval: that is, the intersection is a vertical line segment, a point, or the empty set. More intuitively, a monotone polygon consists of an upper and lower chain, each of which is weakly monotone (hereafter, I simply use monotone to indicate weakly monotone). That is, the points of each chain are already sorted in order of their x-coordinates.

We are concerned here with monotone polygon linkages. A polygon linkage is a set of rigid links (the edges of the polygon) joined at their ends (at the vertices of the polygon) to form a cycle. The important aspect is that the joints are considered to be moveable. Think of a robot arm, a carpenter's ruler, or a cardboard box being folded...
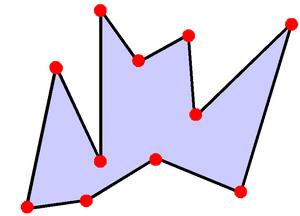
Then we can reconfigure a linkage by changing the angles at some of it's joints while maintining the length of all the links. We will limit allowable reconfigurations to changes that can be applied by a continuous motion which keeps the links from intersecting each other.
The question we want to answer is: Can any monotone polygon be reconfigured into any other monotone polygon with the same link sequence? If we can show that any monotone polygon can be convexified, we can use a result indicating that any convex polygon can be reconfigured into any other convex polygon with the same link sequence to give a positive answer to this question. So the problem becomes: Can any monotone polygon be convexified?
These web pages present a quadratic-time algorithm to convexify a monotone polygon, using a simple type of move which changes the angles at only 4 joints at a time.