How do we know it works ?

We need to verify that the polygon remains simple (the links never intersect) and that it remain monotone during the entire move.

I do not provide a complete proof of the correctness of the algorithm, omitting special cases due to degeneracies (colinearities, etc.) and glossing over some details. My goal here is to give the reader a general idea of the proof. I have marked the arguments where details are omitted with an asterisk, please the paper for a more complete proof.

First we need to make a few observations about the movement we make at each iteration.

Lemma 1: We can always find the four joints needed to execute the move.

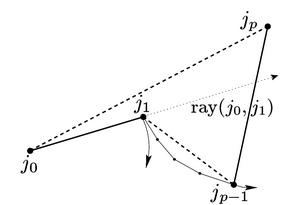
This is guaranteed because j₁ is reflex, so there must be at least one point to the right of the ray ( j₀, j₁ ). So we can always find the points j₀, j₁, j_p-1 and j_p.

Lemma 2: No reflex vertex becomes convex or vice-versa.

We stop the move whenever one of the moving joints straightens, so no joint can go from convex to reflex or vice-versa.

Lemma 3: The joints j₂, ..., j_p-1 are convex.

Since j₁ is the rightmost reflex vertex, any joint to the right of it is convex. Since all the joints j₂, ..., j_p-1 are right of the ray ( j₀, j₁ ) and the polygon is monotone, they are all to the right of j₁, and hence convex.*

Lemma 4: All the angles approach 180º during the motion.

This is a general result for quadrangles with a single reflex vertex whose angle is decreasing. It is intuitively obvious.*

Lemma 5: j_p-1 rotates counterclockwise about j_p during a move.

This follows from lemma 4, since the position of j_p is fixed.

Lemma 6: j₁ rotates counterclockwise about j_p-1

Consider the relative movement of j₁ and j_p about j_p-1. j_p is rotating counterclockwise about j_p-1 and the angle at j_p-1 is increasing by lemma 4, so j₁ must also be rotating counterclockwise about j_p-1.

The Polygon Remains Monotone During a Move

The only way monotonicity can be violated is if a vertical link rotates in the "wrong" direction. That is, in the case of a link on the lower chain, the link ( j_i, j_i+1 ) rotates such that j_i+1 becomes left of j_i. Suppose that one of the moving links ( j_i, j_i+1 ) for 0 ≤ i ≤ p-1 is vertical, can it rotate in the wrong direction? There are three possible cases:

1. Link ( j₀, j₁ ) is vertical: j₁ is reflex and j₂ is right of j₁, so j₁ must be above j₀. Then since j₁ rotates clockwise about j₀, it will not move to the left of j₀, and monotonicity is preserved.

2. Link ( j₁, j₂ ) is vertical: Then j₁ is above j₂ since j₁ is reflex. By lemma 6, j₁ rotates counterclockwise about j_p-1. Hence the triangle j_p-1j₁j₂, which is rigid since the angles are fixed, also rotates counterclockwise about j_p-1. Then the vertical segment j₁j₂ rotates counterclockwise with j₂ below j₁, so j₂ stays to the right of j₁, and monotonicity is preserved.

3. Link( j_i, j_i+1 ) is vertical for some 1 < i < p: We can show that both j_i and j_i+1 are convex by using Lemma 3 and the defintion of j_p.* They remain convex during the move by Lemma 2. Then the joints j_i-1 and j_i+2 are both left of the link ( j_i, j_i+1 )! Otherwise one of the angles would be greater than 180º.
   Since the polygon is monotone up to this point, this must be the link joining the upper and lower chain. No matter how this link moves, the polygon stays monotone.

The Polygon Doesn't Self-Intersect During a Move

First, the moving chain can't intersect itself, since all the angles along it approach 180º and it is monotone. The points along it are becoming more distant from oneanother. So we only need to worry about one of these moving links intersecting the rest of the polygon.

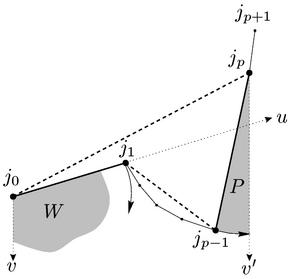
In the figuree above, u is the original position of the ray ( j₀, j₁ ), and v is a downward vertical ray out of j₀. W is the wedge these two vectors define. We are going to show that the only joints in the region W are j₁, ..., j_p-1, and furthermore, that none of these joints ever leave W during a move. This will prove that the links of the moving chain can't intersect the rest of the polygon, except for the link ( j_p-1, j_p ) which we'll deal with later.

First, we show that no joints but the moving joints are inside W. j₀ and j_p are not inside W, so if some other point is, the chain j_p, ...,j₀ must cross either u or v at some point. But:

• the chain can't cross v because that would violate monotonicity;
• the chain can't cross u either, because that would require a reflex vertex somewhere to the right of j₁ if the polygon is monotone.

Now we show that the points j₁, ..., j_p-1 are inside W for the duration of the move. At the beginning of the move, j₁ enters the region since it is rotating clockwise about j₀. The points j₂, ...j_p-1 are all to the right of u by the choice of p, and they are on the right side of v by monotonicity. So at the beginning of the move, the points of the moving chain are inside the wedge W.

We can show that they never leave W. Suppose this were to happen, some joint j_i would have to cross either u or v:

1. Suppose j_i crosses v: j₁ can't be the first to cross v since it stays a reflex vertex during the entire move (by Lemma 2). If some other joint j_i crosses v, then the chain is no longer monotone because j_i will be to the left of j₁ with i > 1. But we just showed that the chain does remain monotone! This is a contradiction, so none of the moving joints can cross v.

2. Suppose j_i crosses u: j₁ can't cross u because it's moving awaig from it. j₂ can't cross u because j₁ is reflex and that entails that j₂ is also moving away from u.
   If j_p-1 crosses u, the move would already have stopped because j₀, j₁ and j_p-1 would have been colinear. So that leaves only j_i for 2 < i < p-1 to cross u first. But then j_i would have to be a reflex vertex, since both it's neighbors are on the other side of u. We know from Lemmas 2 and 3 that these joints all remain convex during a move. So none of the moving joints can cross u.

Now we've shown that none of the links of the chain j₀, ..., j_p-1 can't intersect any of the other moving links, or any of the fixed links. The only remaining possibility of intersection is if the link ( j_p-1, j_p ) intersects one of the fixed links.

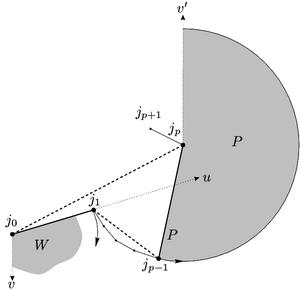
For this, we define v' as a vertical ray pointing away from the interior of the polygon. One possibility is show here, and the other was show in the figure above. Define P as the wedge bounded by the link ( j_p-1, j_p ) and v'. There are no non-moving links inside P by monotonicity. And P contains the entire sweep of the link ( j_p-1, j_p ), since we stop the motion if j_p straightens (in the case where v' points downwards) or if j₀, j₁ and j_p-1 become colinear (in the case where v' points upwards). So the link ( j_p-1, j_p ) can't intersect any part of the non-moving polygon.

We've shown that the polygon remain simple during each move, and that it remains monotone. The running time analysis will show that the motion described does in fact produce a convex polygon, so we can be certain that this algorithm is correct.