

A linkage is a collection of line segments, or links, in the plane which are joined at their ends (joints) to form a graph. Linkages can be reconfigured by a continuous motion of the joints that preserves the length of each link. Here, we enfore that links cannot intersect each other during such motions.
Examples of linkages abound: think of a robotic arm, or the many linkages used in mechanical devices (for instance, to convert a linear motion into a circular motion in an engine.) Or consider a carpenter's ruler which can be folded up, or even the folding of a cardboard box...


The most fundamental question about linkages remained open until recently: Can every chain be reconfigured into any other chain with the same sequence of link lengths? A chain is just a linkage whose underlying graph is a path. We can reformulate this as: Can every chain be straightened? If such is the case, we will be able to move between any two configurations with the same link sequence by first straightening, and then "un-straightenening" the chain, since the motions are reversible.
It seems intuitively clear that any chain can be straightened, but until 2000, no general algorithm for specifying a sequence of motions accomplishing this had been proposed. We can however examine special classes of chains for which the algorithm is obvious: take, for instance, monotone chains, where any vertical line intersects the chain at a single point or non at all. That is, if we traverse the linkage from it's leftmost to it's righmost joint, the points will be encountered in order of ascending x coordinates.
A monotonic chain can be straightened simply by repeatedly rotating the first link so that it lines up with the second, and then fusing these two links into a single new first link.
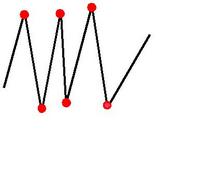
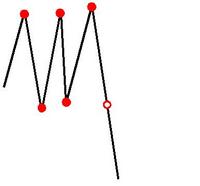
For polygons also, examining special subclasses yielded algorithms before a general convexifying motion was discovered. In 1995 an algorithm for star-shaped polygons was published, and in 1999 an algorithm for monotone polygons was discovered. This later algorithm is presented in these pages.
Finally, in 2000, a general algorithm for polygons was discovered (which also solves the problem for chains and more general planar graphs).
It is interesting to note that it has been shown that the answer to the fundamental problem for tree linkages is negative: there exist trees which cannot be reconfigured into other trees with the same link lengths and underlying graph. In the case of higher dimension polygons, there are unknotted polygons in 3D which cannot be convexified, but it has been shown that every polygon in 4 or more dimensions can be convexified.