The Algorithm

The algorithm is slightly different depending on whether the rightmost reflex vertex is on the upper or lower chain of the polygon. I present the case where it is on the lower chain, the oher case is symmetrical.

Until the polygon is convex:

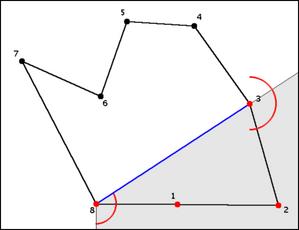
• Find a righmost reflex joint;
  In this example, it's point 1, shown in red.
  

  

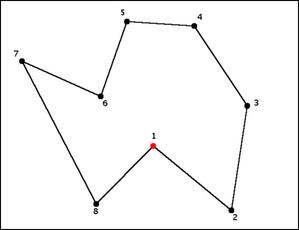
• Relabel the joints counterclockwise along the polygon's perimeter so that this rightmost reflex joint is j₁, and all straight joints are ignored.

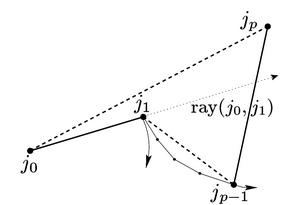
• Find the index p such that j_p is the first joint not on the right of the ray ( j₀, ₁ )
  In this case, it is the joint 4.
  

  

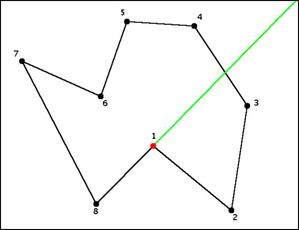
• Perform the move described below until either the joints j₀,j₁, and j_p-1 become colinear, or one of the moving joints straightens. In this instance, we rotate point 1 counterclockwise about point 8, maintaining the lengths of all the links. Only the angles at four points are allowed to change: joints 8, 1, 3 and 4.
  

  

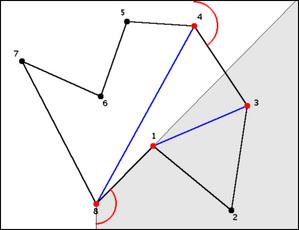
• • If the joints j₀, j₁, and j_p-1 become colinear first, decrement p and continue the move with the new j_p and j_p-1.
    In the example, the joints 8, 1 and 3 become colinear. So joint 3 becomes the new j_p.
    

    

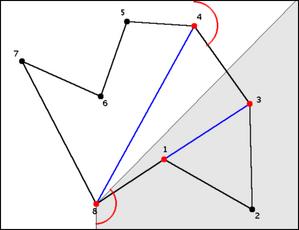
  • If a joint straightens, the iteration is complete, go on to find the new righmost reflex joint.
    In the example shown here, this will happen after we update p and continue the move: the joint 1 straightens. Now one reflex vertex has been straightened.
    

    

The Move

Here j₁ is the rightmost reflex vertex, and j_p is the first joint not to the right of the ray ( j₀, j₁ ).

First we fix the position of all the joints j_p+1 through j_n-1 (which aren't shown here) as well as j₀ and j_p. Then we fix all the joint angles, except for the four joints we will be moving: j₀, j₁, j_p-1 and j_p.

This has for effect of fixing the distances || j₀ j_p || and || j₁ j_p-1 || (shown as dotted lines).

Now simply rotate j₁ clockwise about j₀, the motion of the other two moving joints is uniquely defined since all the link lengths are to be maintained.

Notice that we completely ignore the joints between j₁ and j_p-1 for the move. We can do this because because we have fixed all the angles on that chain, so it can just be considered an edge between j₁ and j_p-1 for the purpose of executing the move.