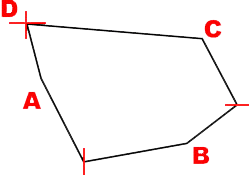
Introduction
The goal of this project is to present an efficient algorithm to compute the largest orthogonal rectangle in a convex polygon. This problem arises when trying to correct the distortion from a misaligned projector. When a rectangular image is projected, it appears as an irregular quadrilateral on the projection surface. To obtain the best possible orthogonal rectangle on the projection surface, we must select the largest one within the projected area. By modeling the projected area as a convex polygon, we can solve the problem by computing the largest inscribed orthogonal rectangle. When multiple projectors are combined to form a large screen, the polygon resulting from the union of all the projected areas might not be convex. We can first clip the polygon and then find the largest rectangle using the same method.
In the next section, we will show that the largest orthogonal rectangle has either two or three corners on the boundary of the polygon. We will then use the algorithm from Alt, Hsu and Snoeyink [1] to find a solution. This involves casting the problem as the search for the fixed-point of a composition of two or three functions. We will also show that the area is maximized at the fixed-point and that we can use a prune-and-search method for the fixed-point of two functions or a tentative prune-and-search for the fixed-point of three functions. Both these methods have a complexity of O(log n). For simplicity, we will assume that the polygon is in general position. i.e. that no two vertices are on the same horizontal or vertical line and that no two edges are parallel. Since all rectangles we will be describing in the following sections are orthogonal, we will use the term rectangle to mean orthogonal rectangle.
Largest Rectangle LR:
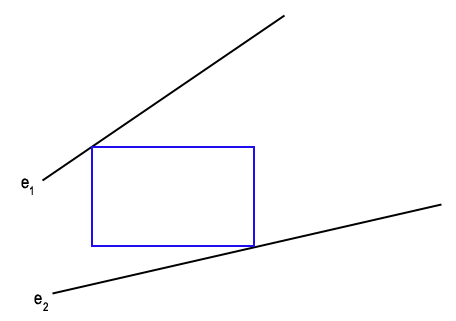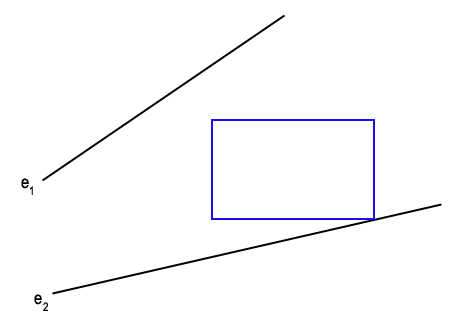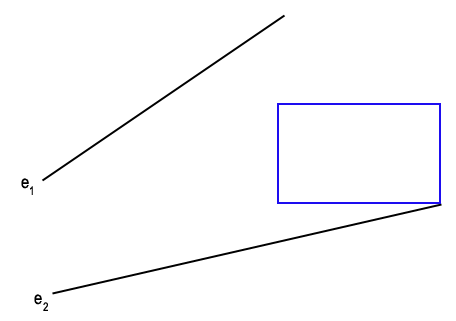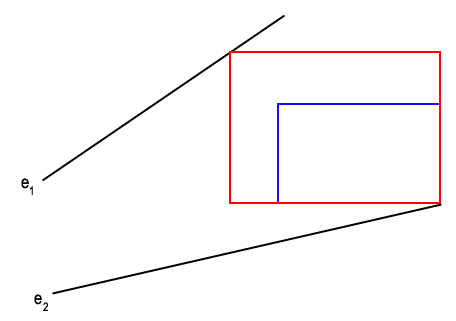
Lemma 1 (from [3]): Let e1 and e2 be non-intersecting line segments. Consider the set of empty axis-parallel rectangles which have diagonnaly opposite corners on e1 and e2. There is a largest area rectangle in this set with at least one corner at an endpoint of e1 or e2.
Proof: In [3], they claim that the 2-parameter area function can be shown to be a saddle surface, and therefore the maximum lies on the boundary. More intuitively, if the general position assumption is satisfied, the two lines containing the line segments will intersect on one side of the line segments. For any rectangle with corners not already on the vertices, it will be possible to slide it in the opposite direction, and then expand it since one of the corners will no longer be in contact with the one edge of the polygon. This can be seen in figure 3 which contains a small animation.
Algorithm
In this section, we describe the algorithm presented in [1] to find the largest area rectangle. If the largest rectangle has exactly two corners on P, then these will lie either on chains A and C or on chains B and D. We obtain the largest rectangle with two corners by looking for both and returning the maximum. We do the same for rectangle with three corners. In this case, there are four possible configurations for the three corners. They can be on A,B,C, or A,B,D or A,C,D or B,C,D. Once we have found all candidates for two and three corners, the maximum of them all will be the largest orthogonal rectangle.
2 corners on the boundary of P:
Lemma 2 (from [1]): Suppose that the maximum area rectangle LR inscribed in P has exactly two corners on the boundary of P, namely a on A and c on C. Then P has parallel tangents at a and c with slope m, where m = -mac.
Proof: If we fix the origin at a, we can get a function of constant area F through c which we can write as F = xy, where x and y are the x and y coordinates of c. Rewritten as y = F/x, we get m, the slope of the tangent at c by taking the derivative dy/dx = -F/x2. The slope of the diagonal from a to c, mac, is y/x or F/x2 when we replace y by F/x. The polygon must have a tangent to c of slope m. If not, we could move c by a small amount to get a rectangle of area larger than F. If the polygon has a tangent to c of slope m, then moving c will only decrease the area of the rectangle. We get the same results by fixing c at the origin and obtaining a function of constant area through a. Combining the two, we get that the tangents at a and c are parallel. An example illustrating this proof can be seen in the animated figure 5. In this example, F = 6, c is located at (3,2). Both the area function and c share a tangent of slope -2/3. The slope of the diagonal is 2/3.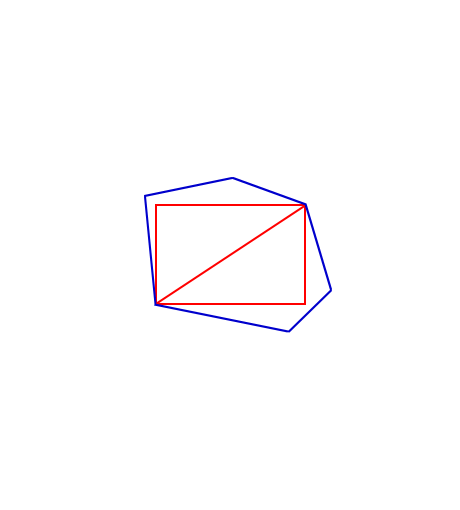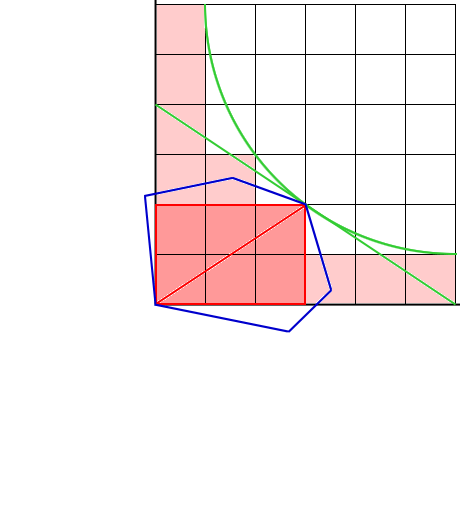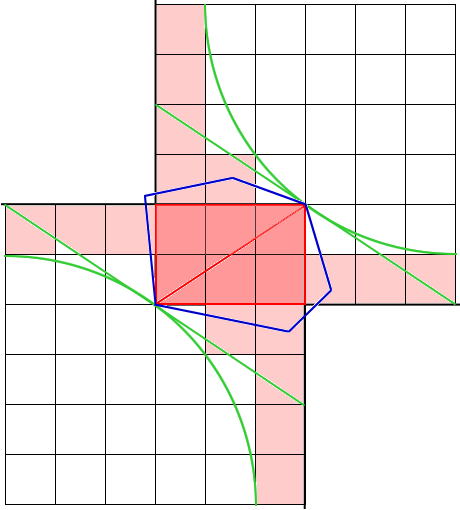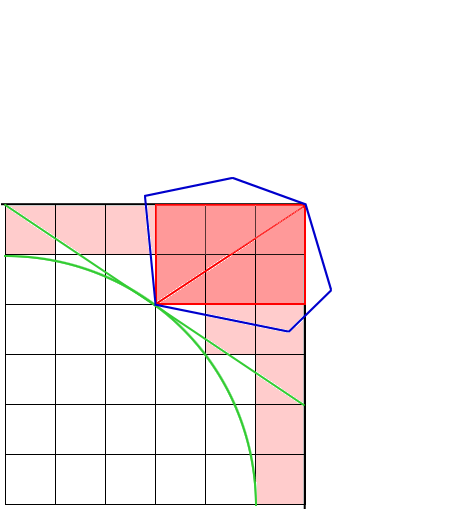
Figure 5 - Parallel tangents to polygon and area function with slope -mac
From lemma 2, we can define two functions f and g, one increasing and the other decreasing, such that the fixed-point of their composition will provide the largest rectangle. For a point a on A, let f(a) be a point on C such the tangents at a and f(a) are parallel. For a point c on C with a tangent of slope m, let g(c) be a point on A, such that the line from g(c) to c has slope -m. When traversing A and C counterclockwise, f is increasing and g is decreasing so their composition has a fixed-point. At the fixed-point, a = g(f(a)) so c = f(a) and g(c) = a. This means that the tangents at a and c are parallel and the slope of the diagonal is negative the slope of the tangent at c. This satifies lemma 2 so the resulting rectangle will be maximized.
Prune-and-search to find the fixed-point of two functions
Now that we have the largest rectangle located at the fixed-point of the composition of two functions, it is necessary to describe how this fixed-point is found. To do so, we place a and c at vertices near the middle of chains A and C and chose one specific value for the tangent out of all the possibilities. By comparing f(a) to c and a to g(c), we can eliminate half of A or C. For example, if f(a) is after c and g(c) is before a, then we can eliminate everything after a since we know the fixed-point cannot be located on that part of A. The function f evaluated for any point on the eliminated chain will always lie above c on C. Evaluating g at this new point will always lie below g(c) on A, which is itself below a, so we will never get back to our original point. All possible cases are presented in the animated figure 6. There are four cases in all, allowing us to eliminate the top or bottom half of A or C. This process can be done without evaluating f(a) or g(c) directly. Instead, to compare f(a) and c, we simply need to compare the tangents at a and c. To compare g(c) and a, we compare the tangent at c to the slope of the diagonal from a to c. Once part of a chain has been eliminated, we pick a new point in the middle of the remaining part. After a logarithmic number of steps, each chain will be reduced to a single edge or vertex. Readers interested in more details about the computation of fixed-points can refer to [2].
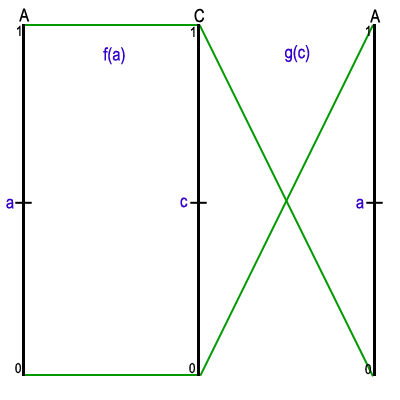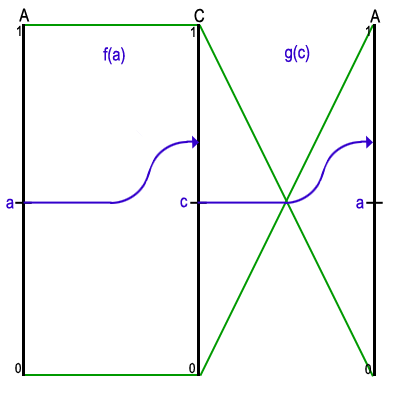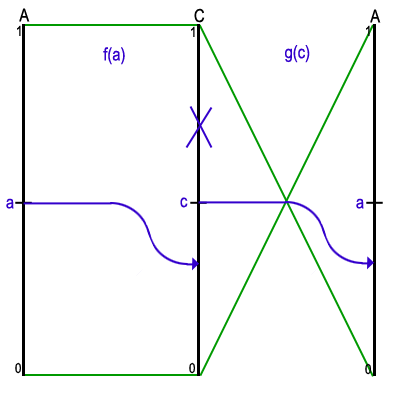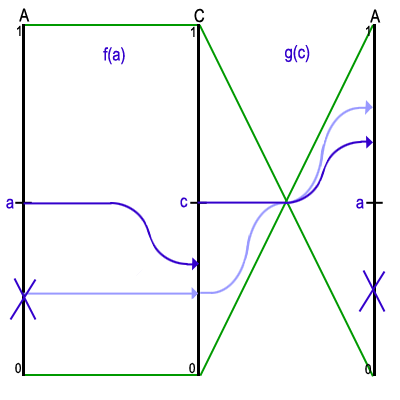
Figure 6 - Prune-and-search for the fixed-point of the composition of two functions
Once both chains have been reduced to a single edge or vertex, it is possible to find the maximum rectangle by simple algebra. For completeness, we will briefly describe how to do this now. If both A and C are reduced to a single vertex, then the largest rectangle has a diagonal connecting the two vertices. If an edge remains on both A and C, from lemma 1, we consider this to be four instances of the case with an edge and a vertex. For this case, the tangent slope is the slope of the edge. We simply need to find a line through the vertex intersecting the edge. This will be the diagonal of the largest rectangle. We then need to test candidates to make sure they are inscribed. This is done by verifying that the two remaining corners are inside de polygon. This can be computed in O(log n) by performing a binary search on chains B and D for the bottom and top corners respectively in order to find the corresponding edge that has the same x (or y) coordinate. Then, in constant time, we can test if the point is inside or not. The largest rectangle with corners on A and C is the maximum of all the valid rectangles. Now that we have the largest rectangle with corners on A and C, we can repeat the same steps to find the largest rectangle with corners on B and D to have the largest rectangle with exactly two corners on the boundary of P. In order to find the largest rectangle overall, we also need to look for the largest rectangle with three corners on P and take the maximum. Figure 7 contains an animation that goes through the entire process of finding a rectangle with two corners on A and C.
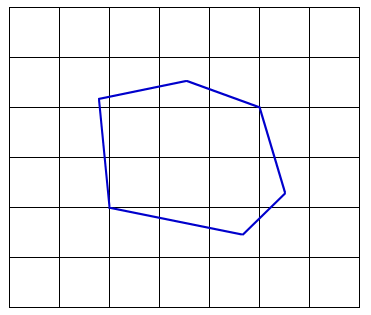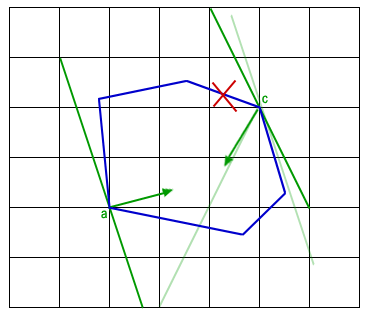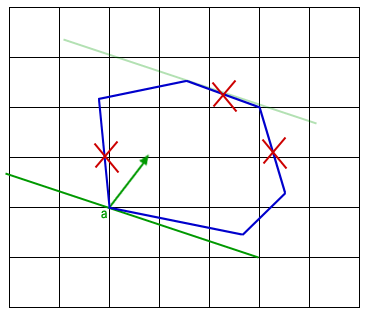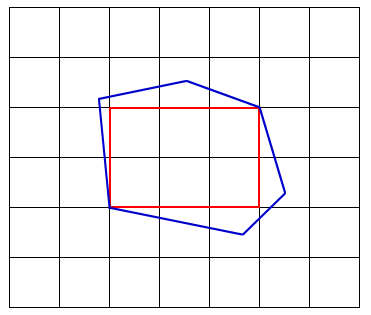
Figure 7 - Example of a rectangle with exactly two corners on the polygon
3 corner on the boundary of P:
Lemma 3 (from [1]): Suppose that the maximum rectangle LR inscribed in P has three corners on the boundary of P. Then, there are tangents at a on A, b on B, and c on C with slopes ma < 0, mb > 0, mc < 0, respectively, that satisfy -ma >= m >= -mc, and m = -ma * (mc - mb) / (ma - mb), where m = mac if LR has maximum area.
The proof of this lemma is somewhat lengthier that for lemma 2 so we will only give some insights and refer interested readers to [1] for all the details. To obtain the equation for m, the area is computed as a function of a, b and c. Taking the derivative, we obtain the maxima and minima when the derivative is zero. When points a and b coincide, the function has a minimum since the area will be equal to zero. The same can be said when points b and c coincide. If we remove with these two cases, we are left with a single zero which corresponds to the maximum. This ultimately leads to the equation for m. Using animated figure 8, we can see that it is necessary for -ma to be greater than -mc. If this is not the case, the rectangle can slide away from b and then be expanded.
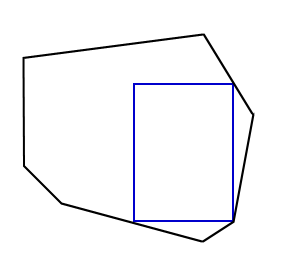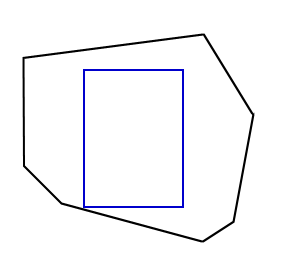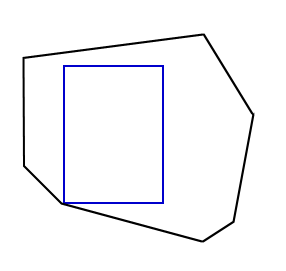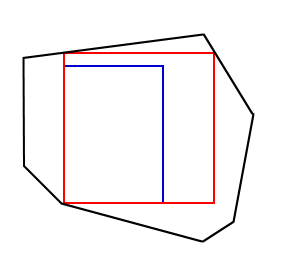
Figure 8 - Rectangle can be made larger if -ma < -mc

Figure 9 - Part of A, B or C can be permanently discarded
However, in two other cases, presented in figure 10, we will only be able to tentatively discard half of all the chains. When there are no tentative discards, we are in normal mode, which is exactly like the two function case. When there are tentative discards, then we enter tentative mode. In this mode, we move a, b, and c in a round robin fashion. The result will either be that nothing changes and we extend the tentative discard, or we are able to permanently discard a portion of one chain. Once a permanent discard has taken place, we can cancel the remaining tentative discards and return to normal mode.
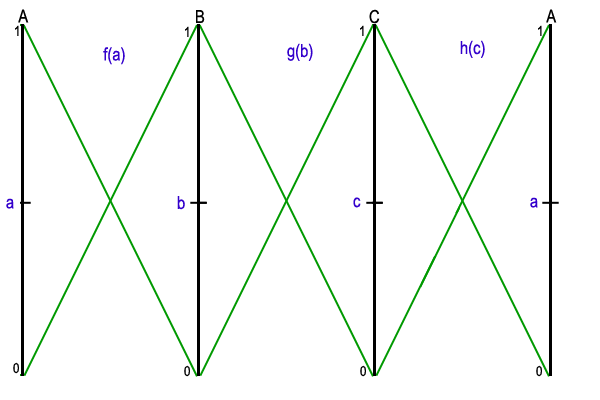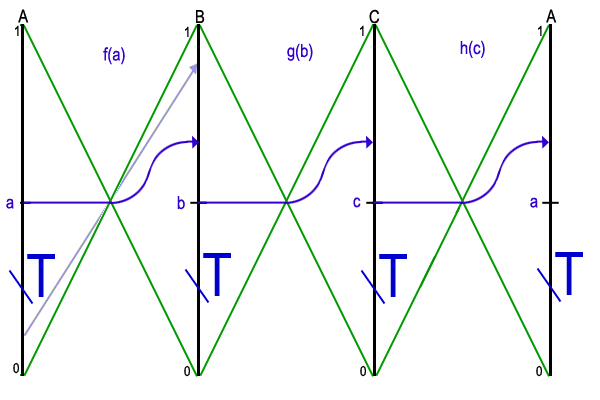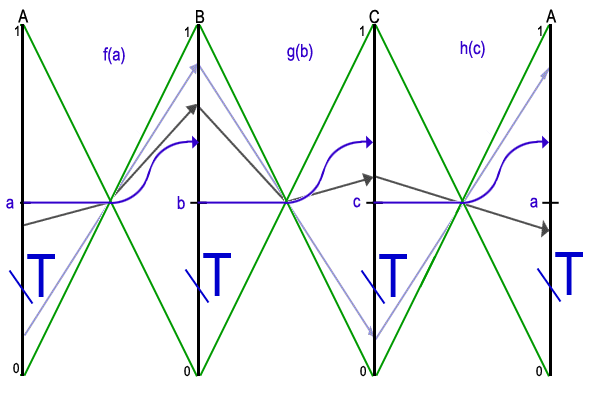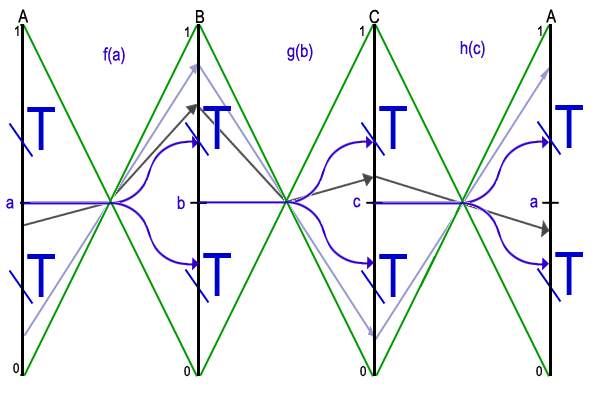
Figure 10 - Part of each of A, B and C is tentatively discarded
Once each chain has been reduced to a single edge or vertex, we can find all candidates for the largest rectangle in constant time using simple algebra. First, there may exist a solution that contains no vertices of P. For this candidate, we need to extend the the edges containing a,b, and c into lines that will intersect to form a triangle. If we parametrize the area as a function of the position of b, we get that the area is maximized when b is located exactly in the middle of its corresponding triangle edge. If this point is on the polygon and so are the corresponding a and c, then this is a valid solution. Other candidates will be contain at least one vertex so we can examine all six of them (two for each edge in A, B and C) and keep only the valid ones. For all the valid candidates, we must make sure they are inscribed exactly like we did when two corners of LR were on P. This will produce the maximum rectangle with corners on A, B and C. We repeat the steps for the three other configurations to obtain the largest rectangle with three corners on the polygon. Comparing the result with the largest rectangle with two corners leads to the largest rectangle overall. Figure 11 shows an example where the largest rectangle has three corners on A, B and C. Since D contains a single vertex, we only need to look for corners on A, B and C when looking for three corners.
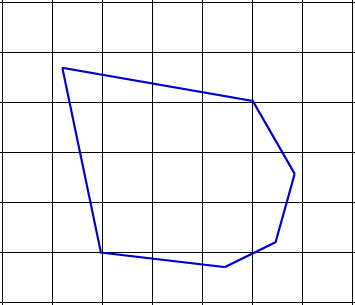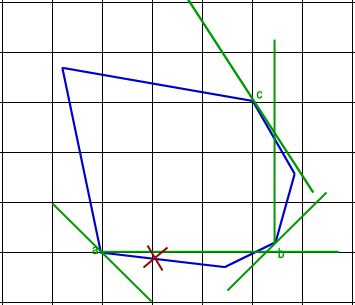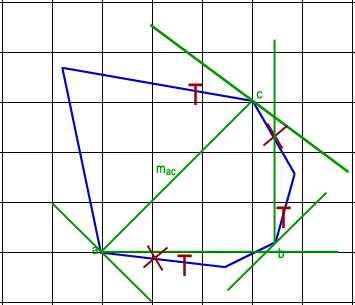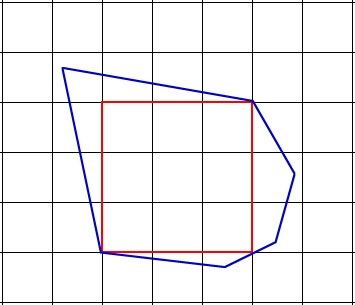
Figure 11 - Example with three corners on A, B and C
Evaluating complexity:
The algorithm presented above has an overall complexity of O(log n), where n is the number of vertices on the polygon. When looking for a rectangle with two corners on A and C, we eliminate half of A or C in each step so these get reduced to a single edge or vertex in log(A+C) < log(n) steps [2]. We then test to make sure each candidate is inscribed in O(log B) + O(log D). We require double this effort to get the largest rectangle with two corners. The complexity of the tentative prune-and-search is evalutated in [1] and [2] using a potential function to show that a non-zero constant number of vertices get discarded at each tentative step. As a result a complexity of O(log n) is achieved to find the fixed-point of three functions. Testing inclusiveness takes O(log D). This is repeated four times to get the largest rectangle with three corners. As a result, the overall complexity is O(log n) and the algorithm presented above is the most efficient known algorithm to find the largest orthogonal rectangle in a convex polygon
Conclusion
The algorithm from [1] presented above can be used to compute the largest orthogonal rectangle in a convex polygon is O(log n). It uses a prune-and-search technique to find the largest rectangle with two corners on the polygon and a tentative prune-and-search to find the largest rectangle with three corners on the polygon. There are two possible configurations for the rectangle with two corners on P that must be evaluated independently and four in the case where the rectangle has three corners on P. These must all be evaluated in order to find the largest rectangle overall.
Alternative Algorithms
- Convex Programming - O(n), [4]
- Nested Binary Search - O(log^2 n), Fischer & Hoffgen
Related Problems
- Computing the largest rectangle in an orthogonal polygon
- Computing the largest inscribed rectangle in any simple polygon [3]
- Computing the largest empty rectangle in a set of points
Applications
- Finding the largest usable screen when projecting from a misaligned projector
- Dense packing. e.g. fitting pieces of clothing on a piece of fabric to minimize waste
Applet Information
Applet Instructions:
Note 2: For rectangles with corners on A and C only or B and D only, if the rectangle displayed does not lie on any vertex, then we know that there exists a larger one and that it will not be inscribed.
Applet source code
Applet
The goal of this project is to present an efficient algorithm to compute the largest orthogonal rectangle in a convex polygon. This problem arises when trying to correct the distortion from a misaligned projector. When a rectangular image is projected, it appears as an irregular quadrilateral on the projection surface. To obtain the best possible orthogonal rectangle on the projection surface, we must select the largest one within the projected area. By modeling the projected area as a convex polygon, we can solve the problem by computing the largest inscribed orthogonal rectangle. When multiple projectors are combined to form a large screen, the polygon resulting from the union of all the projected areas might not be convex. We can first clip the polygon and then find the largest rectangle using the same method.
In the next section, we will show that the largest orthogonal rectangle has either two or three corners on the boundary of the polygon. We will then use the algorithm from Alt, Hsu and Snoeyink [1] to find a solution. This involves casting the problem as the search for the fixed-point of a composition of two or three functions. We will also show that the area is maximized at the fixed-point and that we can use a prune-and-search method for the fixed-point of two functions or a tentative prune-and-search for the fixed-point of three functions. Both these methods have a complexity of O(log n). For simplicity, we will assume that the polygon is in general position. i.e. that no two vertices are on the same horizontal or vertical line and that no two edges are parallel. Since all rectangles we will be describing in the following sections are orthogonal, we will use the term rectangle to mean orthogonal rectangle.
Largest Rectangle LR:
| 2 corners on the boundary of P:
If the largest rectangle LR has exactly two corners on P as in figure 2, then these corners will be diagonally opposed. If the corners were adjacent, then opposite edge of LR would not be touching the boundary of P at all and it could be moved away to form a larger rectangle. Similarly, if a single corner of LR is on the boundary of P, two of the edges of LR would be free to move and form a larger rectangle. Diagonally opposed corners of LR must either be in contact with two vertices of P, or with one vertex and one edge. By lemma 1 (below) and illustrated in figure 3, if neither of the two corners of LR is in contact with a vertex, then a larger rectangle can be found. In the next section, we will show that once the chains containing the two corners have been reduced to a single edge or vertex, then a solution can be found in constant time. |
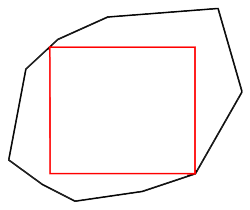
Figure 2. Two corners of rectangle on polygon |
Lemma 1 (from [3]): Let e1 and e2 be non-intersecting line segments. Consider the set of empty axis-parallel rectangles which have diagonnaly opposite corners on e1 and e2. There is a largest area rectangle in this set with at least one corner at an endpoint of e1 or e2.
Proof: In [3], they claim that the 2-parameter area function can be shown to be a saddle surface, and therefore the maximum lies on the boundary. More intuitively, if the general position assumption is satisfied, the two lines containing the line segments will intersect on one side of the line segments. For any rectangle with corners not already on the vertices, it will be possible to slide it in the opposite direction, and then expand it since one of the corners will no longer be in contact with the one edge of the polygon. This can be seen in figure 3 which contains a small animation.

Figure 3. - A two-corner rectangle not on any
vertex of P can be made larger
3 corners on the boundary of P: The largest area rectangle LR may have three corners on the boundary of P, as in figure 4. If the polygon is in general position, at most two corners of LR will be located at vertices of P since adjacent corners cannot both be on a vertex. It is possible for none of the corners to be located on a vertex. In all cases, once each chain has been reduced to a single segment or vertex, we will show in the next section that it is possible compute the largest rectangle in constant time. It may also be possible for the LR to have all four corners on the boundary of P. This rectangle will be found by treating it exactly like the three corner case. |
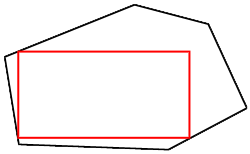
Figure 4 - Three corners of LR on P |
In this section, we describe the algorithm presented in [1] to find the largest area rectangle. If the largest rectangle has exactly two corners on P, then these will lie either on chains A and C or on chains B and D. We obtain the largest rectangle with two corners by looking for both and returning the maximum. We do the same for rectangle with three corners. In this case, there are four possible configurations for the three corners. They can be on A,B,C, or A,B,D or A,C,D or B,C,D. Once we have found all candidates for two and three corners, the maximum of them all will be the largest orthogonal rectangle.
2 corners on the boundary of P:
Lemma 2 (from [1]): Suppose that the maximum area rectangle LR inscribed in P has exactly two corners on the boundary of P, namely a on A and c on C. Then P has parallel tangents at a and c with slope m, where m = -mac.
Proof: If we fix the origin at a, we can get a function of constant area F through c which we can write as F = xy, where x and y are the x and y coordinates of c. Rewritten as y = F/x, we get m, the slope of the tangent at c by taking the derivative dy/dx = -F/x2. The slope of the diagonal from a to c, mac, is y/x or F/x2 when we replace y by F/x. The polygon must have a tangent to c of slope m. If not, we could move c by a small amount to get a rectangle of area larger than F. If the polygon has a tangent to c of slope m, then moving c will only decrease the area of the rectangle. We get the same results by fixing c at the origin and obtaining a function of constant area through a. Combining the two, we get that the tangents at a and c are parallel. An example illustrating this proof can be seen in the animated figure 5. In this example, F = 6, c is located at (3,2). Both the area function and c share a tangent of slope -2/3. The slope of the diagonal is 2/3.

Figure 5 - Parallel tangents to polygon and area function with slope -mac
From lemma 2, we can define two functions f and g, one increasing and the other decreasing, such that the fixed-point of their composition will provide the largest rectangle. For a point a on A, let f(a) be a point on C such the tangents at a and f(a) are parallel. For a point c on C with a tangent of slope m, let g(c) be a point on A, such that the line from g(c) to c has slope -m. When traversing A and C counterclockwise, f is increasing and g is decreasing so their composition has a fixed-point. At the fixed-point, a = g(f(a)) so c = f(a) and g(c) = a. This means that the tangents at a and c are parallel and the slope of the diagonal is negative the slope of the tangent at c. This satifies lemma 2 so the resulting rectangle will be maximized.
Prune-and-search to find the fixed-point of two functions
Now that we have the largest rectangle located at the fixed-point of the composition of two functions, it is necessary to describe how this fixed-point is found. To do so, we place a and c at vertices near the middle of chains A and C and chose one specific value for the tangent out of all the possibilities. By comparing f(a) to c and a to g(c), we can eliminate half of A or C. For example, if f(a) is after c and g(c) is before a, then we can eliminate everything after a since we know the fixed-point cannot be located on that part of A. The function f evaluated for any point on the eliminated chain will always lie above c on C. Evaluating g at this new point will always lie below g(c) on A, which is itself below a, so we will never get back to our original point. All possible cases are presented in the animated figure 6. There are four cases in all, allowing us to eliminate the top or bottom half of A or C. This process can be done without evaluating f(a) or g(c) directly. Instead, to compare f(a) and c, we simply need to compare the tangents at a and c. To compare g(c) and a, we compare the tangent at c to the slope of the diagonal from a to c. Once part of a chain has been eliminated, we pick a new point in the middle of the remaining part. After a logarithmic number of steps, each chain will be reduced to a single edge or vertex. Readers interested in more details about the computation of fixed-points can refer to [2].

Figure 6 - Prune-and-search for the fixed-point of the composition of two functions
Once both chains have been reduced to a single edge or vertex, it is possible to find the maximum rectangle by simple algebra. For completeness, we will briefly describe how to do this now. If both A and C are reduced to a single vertex, then the largest rectangle has a diagonal connecting the two vertices. If an edge remains on both A and C, from lemma 1, we consider this to be four instances of the case with an edge and a vertex. For this case, the tangent slope is the slope of the edge. We simply need to find a line through the vertex intersecting the edge. This will be the diagonal of the largest rectangle. We then need to test candidates to make sure they are inscribed. This is done by verifying that the two remaining corners are inside de polygon. This can be computed in O(log n) by performing a binary search on chains B and D for the bottom and top corners respectively in order to find the corresponding edge that has the same x (or y) coordinate. Then, in constant time, we can test if the point is inside or not. The largest rectangle with corners on A and C is the maximum of all the valid rectangles. Now that we have the largest rectangle with corners on A and C, we can repeat the same steps to find the largest rectangle with corners on B and D to have the largest rectangle with exactly two corners on the boundary of P. In order to find the largest rectangle overall, we also need to look for the largest rectangle with three corners on P and take the maximum. Figure 7 contains an animation that goes through the entire process of finding a rectangle with two corners on A and C.

Figure 7 - Example of a rectangle with exactly two corners on the polygon
3 corner on the boundary of P:
Lemma 3 (from [1]): Suppose that the maximum rectangle LR inscribed in P has three corners on the boundary of P. Then, there are tangents at a on A, b on B, and c on C with slopes ma < 0, mb > 0, mc < 0, respectively, that satisfy -ma >= m >= -mc, and m = -ma * (mc - mb) / (ma - mb), where m = mac if LR has maximum area.
The proof of this lemma is somewhat lengthier that for lemma 2 so we will only give some insights and refer interested readers to [1] for all the details. To obtain the equation for m, the area is computed as a function of a, b and c. Taking the derivative, we obtain the maxima and minima when the derivative is zero. When points a and b coincide, the function has a minimum since the area will be equal to zero. The same can be said when points b and c coincide. If we remove with these two cases, we are left with a single zero which corresponds to the maximum. This ultimately leads to the equation for m. Using animated figure 8, we can see that it is necessary for -ma to be greater than -mc. If this is not the case, the rectangle can slide away from b and then be expanded.

Figure 8 - Rectangle can be made larger if -ma < -mc
Tentative prune-and-search to find the fixed-point
of three functions
Using lemma 3, we now need to define three functions so
that their fixed-point will reveal the largest rectangle with three corners
on P. For this we need all three functions to be decreasing when
traversing P counterclockwise. Naturally, we can define f(a)
to be the point on B with the same y coordinate as a on A. Similarly,
g(b) to be the point on C with the same x coordinate as b
on B. Finally, let h(c) be the point on A such that
mac = m as in lemma 3. Like
in the two corner case, we do not need to evaluate f, g, or
h directly. We obtain f(a) and g(b) trivially
since these are the y coordinate of a and the x coordinate of b
respectively. To evaluate h(c), we compare the slope of the
line from a to c to m computed using the equation from
lemma 3. Figure 9 shows that in most of the cases, six out of
eight actually, we will be able to eliminate half of one of the three chains,
exactly like we did for the case with two functions.

Figure 9 - Part of A, B or C can be permanently discarded
However, in two other cases, presented in figure 10, we will only be able to tentatively discard half of all the chains. When there are no tentative discards, we are in normal mode, which is exactly like the two function case. When there are tentative discards, then we enter tentative mode. In this mode, we move a, b, and c in a round robin fashion. The result will either be that nothing changes and we extend the tentative discard, or we are able to permanently discard a portion of one chain. Once a permanent discard has taken place, we can cancel the remaining tentative discards and return to normal mode.

Figure 10 - Part of each of A, B and C is tentatively discarded
Once each chain has been reduced to a single edge or vertex, we can find all candidates for the largest rectangle in constant time using simple algebra. First, there may exist a solution that contains no vertices of P. For this candidate, we need to extend the the edges containing a,b, and c into lines that will intersect to form a triangle. If we parametrize the area as a function of the position of b, we get that the area is maximized when b is located exactly in the middle of its corresponding triangle edge. If this point is on the polygon and so are the corresponding a and c, then this is a valid solution. Other candidates will be contain at least one vertex so we can examine all six of them (two for each edge in A, B and C) and keep only the valid ones. For all the valid candidates, we must make sure they are inscribed exactly like we did when two corners of LR were on P. This will produce the maximum rectangle with corners on A, B and C. We repeat the steps for the three other configurations to obtain the largest rectangle with three corners on the polygon. Comparing the result with the largest rectangle with two corners leads to the largest rectangle overall. Figure 11 shows an example where the largest rectangle has three corners on A, B and C. Since D contains a single vertex, we only need to look for corners on A, B and C when looking for three corners.

Figure 11 - Example with three corners on A, B and C
Evaluating complexity:
The algorithm presented above has an overall complexity of O(log n), where n is the number of vertices on the polygon. When looking for a rectangle with two corners on A and C, we eliminate half of A or C in each step so these get reduced to a single edge or vertex in log(A+C) < log(n) steps [2]. We then test to make sure each candidate is inscribed in O(log B) + O(log D). We require double this effort to get the largest rectangle with two corners. The complexity of the tentative prune-and-search is evalutated in [1] and [2] using a potential function to show that a non-zero constant number of vertices get discarded at each tentative step. As a result a complexity of O(log n) is achieved to find the fixed-point of three functions. Testing inclusiveness takes O(log D). This is repeated four times to get the largest rectangle with three corners. As a result, the overall complexity is O(log n) and the algorithm presented above is the most efficient known algorithm to find the largest orthogonal rectangle in a convex polygon
Conclusion
The algorithm from [1] presented above can be used to compute the largest orthogonal rectangle in a convex polygon is O(log n). It uses a prune-and-search technique to find the largest rectangle with two corners on the polygon and a tentative prune-and-search to find the largest rectangle with three corners on the polygon. There are two possible configurations for the rectangle with two corners on P that must be evaluated independently and four in the case where the rectangle has three corners on P. These must all be evaluated in order to find the largest rectangle overall.
Alternative Algorithms
- Convex Programming - O(n), [4]
- Nested Binary Search - O(log^2 n), Fischer & Hoffgen
Related Problems
- Computing the largest rectangle in an orthogonal polygon
- Computing the largest inscribed rectangle in any simple polygon [3]
- Computing the largest empty rectangle in a set of points
Applications
- Finding the largest usable screen when projecting from a misaligned projector
- Dense packing. e.g. fitting pieces of clothing on a piece of fabric to minimize waste
Applet Information
Applet Instructions:
- Click on points in the middle region to generate a convex hull.
- Click on "Find Largest Rectangle" to obtain a solution
- Click on "Step" to cycle through largest rectangle with corners on AC only, BD only, ABC, ABD, ACD and BCD.
- It is possible to modify the polygon after finding the largest rectangle
to observe the changes on the largest rectangle
Note 2: For rectangles with corners on A and C only or B and D only, if the rectangle displayed does not lie on any vertex, then we know that there exists a larger one and that it will not be inscribed.
Applet source code
Applet