Shallow selection by the line sweep technique of Bentley and Ottman

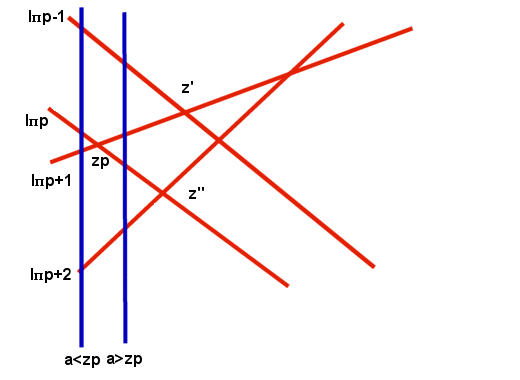
The sweep starts at x = a, a< t₁. Let pi be the number of permutation that sort the slopes in ascending order. Thus m_pi1 <…<mpi_n, where we write y = m_ix+b_i as a equation of l_i. If a< t₁, the vertical line x=a meets l₁,…, l_n, at y₁(a),…, y_n(a) and y_pi1(a)>…> y_pin(a). For each adjacent pair of lines, find the x-coordinate z_i = (b_pii - bpi_i+1)/(mpi_i – mpi_i+1) of their intersection point and place these n-1 numbers in a (min) heap. Clearly t₁ = min(z_i).

Suppose z_p is the smallest z_i. It is currently at the top of the heap. We sweep juste beyond t₁=z_p. When a> t₁, y_pip(a) < ypi_p+1(a) because l_pip and lpi_p+1 have crossed at t₁. We compute the two new intersection points z' = (bpi_p+1 – bpi_p-1)/(mpi_p+1 – m_pip-1) and z'' = (bpi_p+2 – b_pip)/(mpi_p+2 – mpi_p) (if p=n-1, only conpute z'; if p=1, only compute z''). We delete z_p from the heap, insert z' and z'', and exchange _p and _p+1 . We may now obtain t₂ = min(z_i) having expended O(logn) steps. The two new z's were computed in constant time, and the deletion and two insertions took O(logn) time. We continue in the same fashion by sweeping through to t_k.

So the running time is O(nlogn+klogn). O(nlogn) for the starting (min) heap and O(klogn) for the insertions , computation of the z's and deletions, which are applied until we find t_k (so k steps).