The general selection algorithm with a O(n(logn)2)-time complexity
Introduction
We
write pi(a) for the permutation that orders the intercepts
of l1,…, ln, in descending order at x=a. So
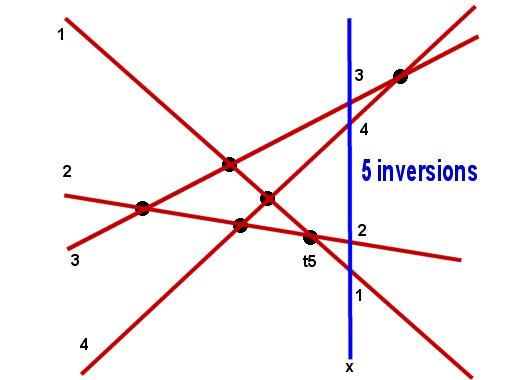
ypi1(a)>…> ypin(a). We renumber l1,…, ln so that for a< t1, (a) is the identity. The permutation
pi(t1) has one inversion (exactly one
paire of lines crossed at t1), pi (t2) has two, etc…
In
fact the function I( (x)) =
number of inversions in pi(x), is
a monotone step function in x with unit jumps at the ti's.
I(pi (x)) = j if and only if tj = max(ti:ti<=x).
For a given k, the problem of finding
tk may be viewed as an usual sorting
problem to which we apply Megiddo's technique of building algorithms from
parallel ones. An implicit binary search over the ti's is performed,
each step taking O(nlogn) time. This will an O(n(logn)2)-time
algorithm.
Presentation
of the algorithm
In
seeking tk , we will attempt to sort y1(a*),…,
yn(a*) at a* = tk +
epsilon. We know that this sort may be achieved in O(nlogn) comparisons
(cf Binary Search Tree), each answering a question Qij of the form "yi(a*)<=yj(a*)?". The O(nlogn) answers yield
the permutation pi* that
sorts these intercepts : ypi*1(a*)>…> ypi*n(a*).
Once pi*
has beed found, tk = max[upii*pii+1*:pii*>pii+1*]; the kth inversion must have just
reversed a pair of adjacent intercepts in the permutation pi(tk-1).
The
control structure for the sort will come from the O(logn)-depth sorting
network of Ajtai, kmlos and Szemeredi (AKS-Network). At each level, n/2
questions are answered. The network is just a guide for blocking these
comparisions into groups of size n/2. The sort is complete once the O(nlogn)
answers are obtained and we have determined pi*.
Even
though we do not know a*, we can answer
the question Qij
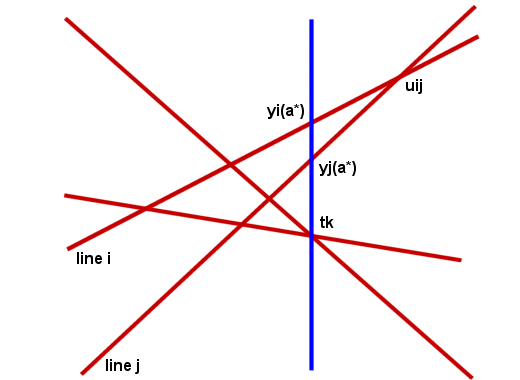
in time O(nlogn) as follows. We find uij
the x-coordinate of , li inter lj , i<j,
in constant time and then obtain its rank among the ti's.To find its rank, we sort the n intercepts
at uij in decreasing
order to get pi(uij). The rank uij is the number of inversions in pi(uij), I(pi
(uij)).
If
I(pi (uij))>k, we know that uij> tk so the answer is "no"; lines i and
j have not yet crossed at tk.
If
I(pi(uij))<k, we know that uij< tk so the answer is "yes".
If
I(pi (uij))=k, uij=tk.
I may be computed in time O(nlogn) (merge sort of Knuth) : if pi(uij) = (r1,…,rn), we use merge-sort to sort the slopes mr1,…,mrn and count the number of inversions that were performed.
If
we actually answered all n/2 questions Qi1j1,…, Qinjn on a level of the network by counting
inversions, the complexity would be O(n2logn) for that level
(n/2 questions*2nlogn for the sort of the n intercepts and the merge sort).
And as there are O(logn) levels, we have a complexity of O((nlogn)2)
overall.
Improvements
The trick is to resolve the n/2 questions on a level by actually counting inversions only O(log) times.
As mentionned, each questions determines an intersection of a distinct pair of lines, and the answer is obtained by comparing the rank of that intersection point with k.
On
a given level of the sequentialzed version of the sorting network, denote
the x-coordinates of these points by zi1,…,zin/2.
We can compute the median of these intersections points, zmed,
in time O(n). Its cost time O(nlogn) to rank it, and answer half the questions.
For example, if zmed < tk, then zik <
tk for all the zik ≤ zmed. Continuing with the n/4
unresolved questions on this level, we again find the median z and rank
it in time O(nlogn), etc…After O(logn) inversions counts, all n/2 questions
on this level are resolved. Since each inversion count takes O(nlogn)
steps and there are O(logn) levels, the algorithm has time complexity
O(n(logn)3).
But,
Cole shows how the result may be improved by a factor of logn, by considering
the fact that in the network each question has two inputs. (see R.COLE,
Slowing down sorting networks to obtain faster sorting algorithms,
Journal of the.ACM, No34 (1987), pp200-208)
So we obtain an algorithm of O(n(logn)2)-time complexity