Dual Problem

Given n points (x₁, y₁),…, (x_n, y_n). We assume that the points are in general position, that means that no three points are colinear and that no two of the induced lines have the same slope.This assumption symplify the problem without affecting the complexity of the algorithms.

To make progress in designing selection algorithms, we transform the slope selection problem into a more convenient form using point-line duality.

This is defined by a mapping T that takes the point p = (a,b) to the line Tp given by y=ax+b and the line l given by y = cx+d to the point (-c,d). T preserves incidence.

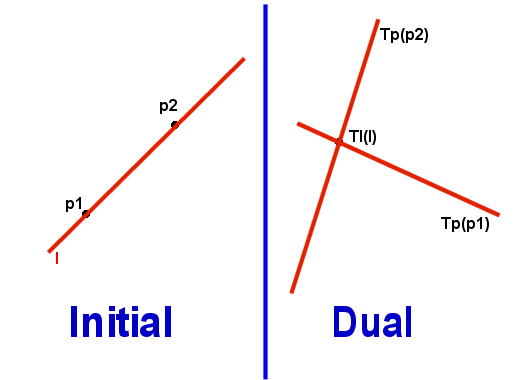
Under T, the n given points map to lines l₁,…, l_n whose points of intersection , l_i inter l_j = (u_ij ,v_ij), correspond to the lines incident with ith and jth original points. Furthermore -u_ij is the slope of this line. Thus the dual of the problem of selecting slope k is the following, equivalent selection problem:

Given distinct l₁,…, l_n, lines, find the intersection point whose x-coordinate is the N-k+1th smallest element of the set TS = {u_ij, 1 <= i< j<= n}.

Now, we will consider the general problem of selecting elements in TS.

We write t₁<…<t_N for the N elements of TS. The ti's are distinct because the input points are in general position. Given k, we seek t_k.