Improvement
with approximate ranking
The new idea
We use an approximate rank for each point chosen by the sorting network.
Let
sign(x) = 1 if x>0, 0 if x=0, and –1 if x<0.
In the improved algorithm, we will use O(n) time to develop an approximation
roz to the rank of z. Let ez
denote the error of approximation : ez=|rank(z)-roz|. If the error is small enough, roz can tell us the relative ordering of
z and tk. By definition, rank(z) must lies inside the closed
interval [roz-ez,roz+ez], then sign(z- tk)
= sign(rank(z)-k) = sign(roz -k); in this case the relative ordering
of z and tk can be deduced from roz and k, and we may resolve
the relevant zi's.
On
the other hand, if lies inside [roz-ez,roz+ez], the approximation will
not be accurate enough to distinguish the relative position of z and tk,
so we must do some extra comparisons to refine roz and reduce ez, until k lies outside the interval. It turns
out that most O(nlogn) extra work will be done to refine rank approximations
throughout the entire course of the algorithm.
The key structure
Suppose
we have a "reference" point at x=r and we know sign(rank(r)
- tk). Also suppose that we have partitioned the n lines into
tau = E[n/T] groups G1,…,Gtau
of size T (maybe Gtau is smaller and T is an integer to be specified) with the property
that if k belongs to Gi and l belongs to Gj, and i<j, then yk(r)<=yl(r).
Thus,G1 refers to the lines with the T largest intercepts at x=r, etc…The groups are therefore sorted, but within any particular group, we have no ordering information. Such a structure is called a partition of size T at r. The occasional refinements will divide T by 2 and restore the reference point in time O(n).
A partition of siwe T at r is represented by a permutation p(r,T).
p(r,T)
= (p1(r,T),..., pn(r,T)), where (p1(r,T),...,
pT(r,T)) are the lines in G1, etc…
Partition p(r,T) is thus an approximation to pi(r). So we define the approximate rank ro(r,T) to be the number of inversions in p(r,T).
Because p(r,T) represents the partition, it can differ from pi(r) only with respect to inversions between pairs of lines within the same group.There are at most "T choose 2" such inversions in a group, there are n/T groups so ro(r,T) differs from rank(k) by less than nT/2. Therefore, for any given value of T, ez <nT/2.
Let T such that, |ro(r,T)-k|<=nT and |ro(r,T/2)-k|>nT/2.
From
the last condition, we are able to determine the relative position of
r and tk. If these conditions fail for the current
value of T, we would halve T and create the partition for the new smaller
groups.
Moreover,
these two conditions imply the fact that nT/4<|rank(z)-k|<3nT/2.
The flow
of control
We
now describe the flow of control in the approximation algorithm. The algorithm
maintain two reference points : rL<=tk and rR>=tk. We maintain orderings p(rL) and p(rR) and calibrated partition sizes TL
and TR for both reference points. The reference with
the smaller T is "active".
When
the network gives a new query point x=q (weighted median point of n/2
points), if q lies outside [rL, rR], the relative position of q with
respect to tk, may be deduced by transivity. We can resolve
this point and the relevant zi's of wich q was the weighted median.
Otherwise we construct the partition of x=q.
If q< tk, the partition of size T at q is a modification of the partition of size T at rL.
If
q> tk, the partition of size T at q is a modification of the partition of size
T at rR.
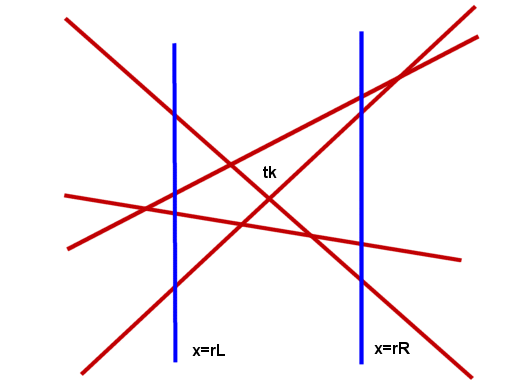
But
we do not know the relative ordering of q, an attempt is to modify the
partition at r, the active reference point. The attempt will be aborted
if |rank(r)-rank(q)| is "large"; in this case, the other reference
point becomes active and the partition at this reference point is modified
to give the partition at q.
Position q then replaces the appropriate reference point (on the same side of tk), and the reference point with smallest value of T becomes the new active reference point.
We claim that this algorithm has an O(nlogn)-time complexity for any k. (proof by the correctness and the computation of each function, for example, partition, of this algorithm)