Maurice Fréchet (1878-1973)
By Stéphane Pelletier
Computational Geometry 308-507A
McGill University
Fall 2002
Note : This web page requires the plugin for Java 2 v1.4.1
In object recognition applications, the objects of interest are often modelized in the system database by their
shape, and thus, an important step of the recognition process consists generally to look for known shapes in an
image.
In many applications, two-dimensional shapes are given by the planar curves forming their boundaries.
Consequently, a natural problem in shape comparison and recognition is to measure how much two given
curves resemble
each other. Naturally, the first question to be answered is what distance measure
between curves should be used to reflect the intuitive notion of resemblance.
One possibility consists in approximating each curve by a set of points and then using the Hausdorff distance, which is defined as follows:
|
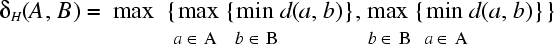
(eq. 1) |
where d is the underlying metric in the plane, for example the Euclidian distance, and A and B are the two sets of points describing the two curves to be compared. While the Hausdorff distance is an appropriate measure in many applications, the following figure shows an example where it is not. The two curves have a small Hausdorff distance, but do not look like each other at all.
The reason of this discrepancy is that the Hausdorff distance only takes into account the sets of points on both curves and does not reflect the course of the curves. However, the course of curves is important in many applications, for example in handwriting recognition. In order to overcome this problem, one can use the Fréchet distance, that was first defined by Maurice Fréchet (1878-1973).
The Fréchet distance can be illustrated as follows : suppose a man is walking his dog and that he is constrained to walk on a curve and his dog on another curve. Both the man and the dog are allowed to control their speed independently, but are not allowed to go backwards. Then, the Fréchet distance of the curves is the minimal length of a leash that is necessary.
As performing mathematical operations on a curve of arbitrary shape turns out to be difficult in some cases,
it is often useful to approximate a curve by a polygonal curve.
A polygonal curve P:[0, N] is a continuous and piecewise linear curve made of N connected segments.
Such a curve can be parametrized with a parameter a 
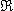such
that P(a) refers to a given
position on the curve, with P(0) refering to the first vertex of the polygonal curve and P(N)
refering to its last vertex, as shown in the following figure.
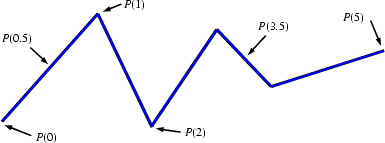
Now, suppose that the man of the previous example is constrained to walk on a polygonal curve P of length N and that his dog has to walk on a polygonal curve Q of length M. The position of the man and the dog on their respective curve can be modelized as a function of t by using two continuous and increasing function α(t) and β(t), where α(0) = 0, α(1) = N, β(0) = 0 and β(1) = M. The position of the man as a function of time is given by P(α(t)) and the position of the dog by Q(β(t)). While many functions α(t) and β(t) can be used, some of them will cause the distance between the dog and the man to be large at some instant, whereas other functions will not. Finding the Fréchet distance actually corresponds to find two parametrization functions α(t) and β(t) that minimize the maximum distance between the man and his dog.
The following applet illustrates the effect of α(t) and β(t) on the maximum distance. Select one of the two examples, click on the run button and observe how the cursors move along the curves. You will notice that the maximum distance between the two cursors is not the same for both examples.
Mathematically, the Fréchet distance between two curves is defined as
|
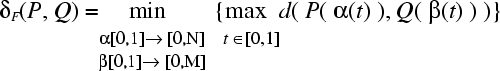
(eq. 2) |
where α(t) and β(t) range over continuous and increasing functions with α(0) = 0, α(1) = N, β(0) = 0 and β(1) = M only.
This equation reads like: for every possible function α(t) and β(t), find the largest distance between the man and its dog as they walk along their respective path; finally, keep the smallest distance found among these maximum distances.
For simplicity, we'll take d(a,b) as the Euclidian distance between a and b.
In a first time, let's consider an easier variant of the problem, namely the following decision problem:
Given: polygonal curves P and Q and some ε ≥ 0
Decide: whether δF(P,Q) ≤ ε
Throughout the rest of this tutorial, let P:[0,p] and Q:[0,q] be polygonal curves. Therefore, p and q are the number of edges of P and Q respectively. In order to solve the decision problem, let us first consider the case where p = q = 1, i.e. P and Q are just simple segments. We define
|
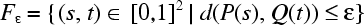
(eq. 3) |
that describes all pairs of points, one on P, one on Q, whose distance is at most ε. The following figure shows line segments P, Q, a distance ε > 0, and Fε being the white area within the unit square; subsequently called the free space.
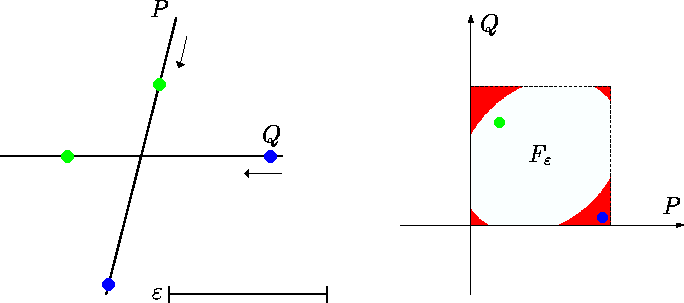
As the distance between the two green points on the curves is smaller than ε, the corresponding green point in the unit square belongs to the free space. Conversely, the blue point in the unit square does not belong to the free space, as the distance between the two corresponding blue points on the curves is larger then ε. Also, the free space corresponding to two line segments is the intersection of the unit square with an ellipse, possibly degenerated to the space between two parallel lines. The proof of this can be found in [1]. The important thing to remember here is that the free space of two line segments is convex.
We can extend equation 3 to arbitrary polygonal curves P, Q, of length p, q respectively:
|
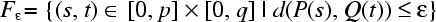
(eq. 4) |
The free space corresponding to the curves P and Q is the combination of the free spaces of all pairs containing one segment of P and one segment of Q. The following figure shows two polygonal curves and their corresponding free space for a given value of ε.
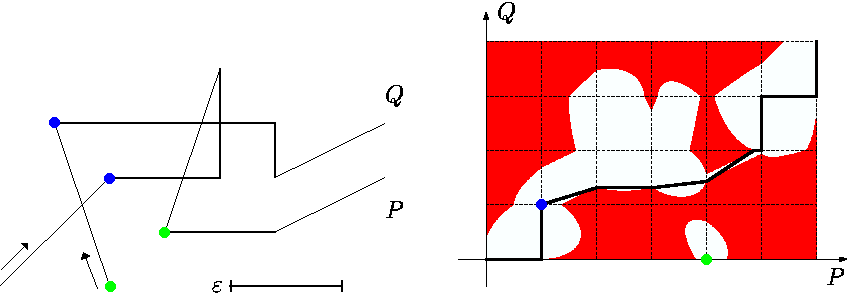
The algorithm is based on the following straightforward observation:
For polygonal curves P and Q we have δF(P, Q) ≤ ε, exactly if there exists a curve within the corresponding Fε from (0, 0) to (p, q) which is monotone in both coordinates.
In the man-dog example, the monotonicity condition corresponds to the fact that none of them is allowed to go backwards. Figure 3 shows such a curve proving that for that example the Fréchet distance is lower than ε.
Now, let Fε(i, j) with 1 ≤ i ≤ p, 1 ≤ j ≤ q refer to the free cell corresponding to the segment P(i - 1) P(i) and the segment Q(i - 1)Q(i). What we are interested in at this point is to find the intersection of the free space with the contour of each Fε(i, j). If the free space intersects the edge of a cell, it means that it is possible to enter in that cell through this edge. As the free space of each unit cell is convex, it is an easy matter to determine if there is a monotone curve that goes from (0,0) to (p, q) by computing all the intersections of the free space with the contour of each cell. The following figure illustrates the values that must be calculated in order to identify the passages between neighboring cells. LFi,j refers to the left line segment bounding Fε(i, j) and BFi,j refers to the bottom line segment.
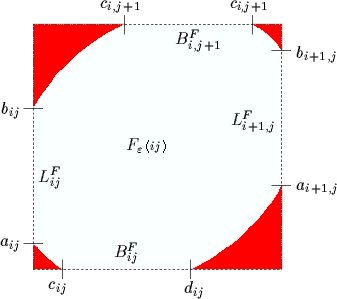
Furthermore, we define
|
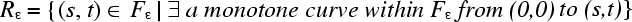
(eq. 5) |
The following figure shows the difference between Fε and R ε. One can see that all the zones that were not reachable by a monotone curve in Fε have been removed in Rε. Hereafter, Rε will be referred to as the monotone free space.
Rε can easily be computed from Fε. We will use almost the same notation as in figure 5 above to designate the values that have to be calculated for the monotone free space. That is, LRi,j will refer to the left line segment bounding Rε(i, j) and BRi,j will refer to the bottom line segment.
yesif (p, q)
LRp+1, q
nootherwise.
The values of figure 5 can be calculated in constant time for each free space cell by using any algorithm that computes segment-circle intersections. Therefore, if polygonal curves P and Q respectively have p and q segments, then the previous algorithm decides in O(pq) time, whether δ F(P,Q) ≤ ε.
Now, let us consider the problem of really computing the Fréchet distance. Assume that we start with ε = 0 and continuously increase ε. Then the free space becomes larger and larger and we want to determine the smallest ε such that it contains a monotone curve from (0,0) to (p,q). Observe that this can occur only in one of the following cases:
Fε and
(p,q) FεClearly, case a) states that δF(P,Q) must be greater or egal to the distance between the starting points of P and Q and also greater or egal to the distance between their ending points. Case b) corresponds to the opening of a new passage between two neighboring cells and case c) corresponds to the opening of a new vertical or horizontal passage within the diagram. The following figure illustrates case c) for a horizontal passage.
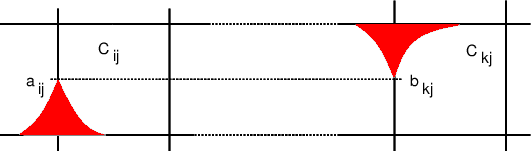
The following figure shows the geometric meaning of ε in cases a), b) and c).
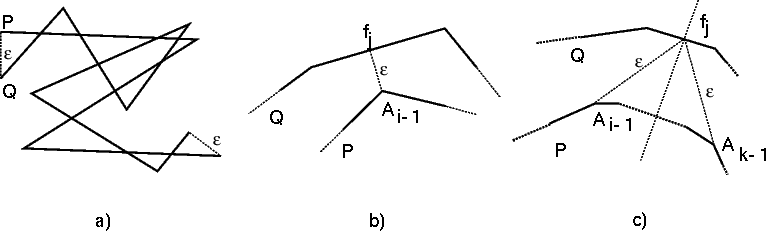
There are O(p2q + pq2) such critical values of ε, namely the distance between starting points and endpoints of P and Q (case a), the distances between vertices of one curve and edges of the other (case b), and the common distance of two vertices of one curve to the intersection point of their bisector with some edge of the other (case c). Each one of these values can be computed in O(1) time. So, we obtain the following algorithm for computing δF(P,Q).
We observe that the runtime is majorized by the one of step 2, which is O((p2q + q2p)log(pq)).
The following applet illustrates the algorithm. For simplicity reasons, the implemented algorithm doesn't calculate the critical values of ε that correspond to case c).