| Previous | Demonstration | About | Next |

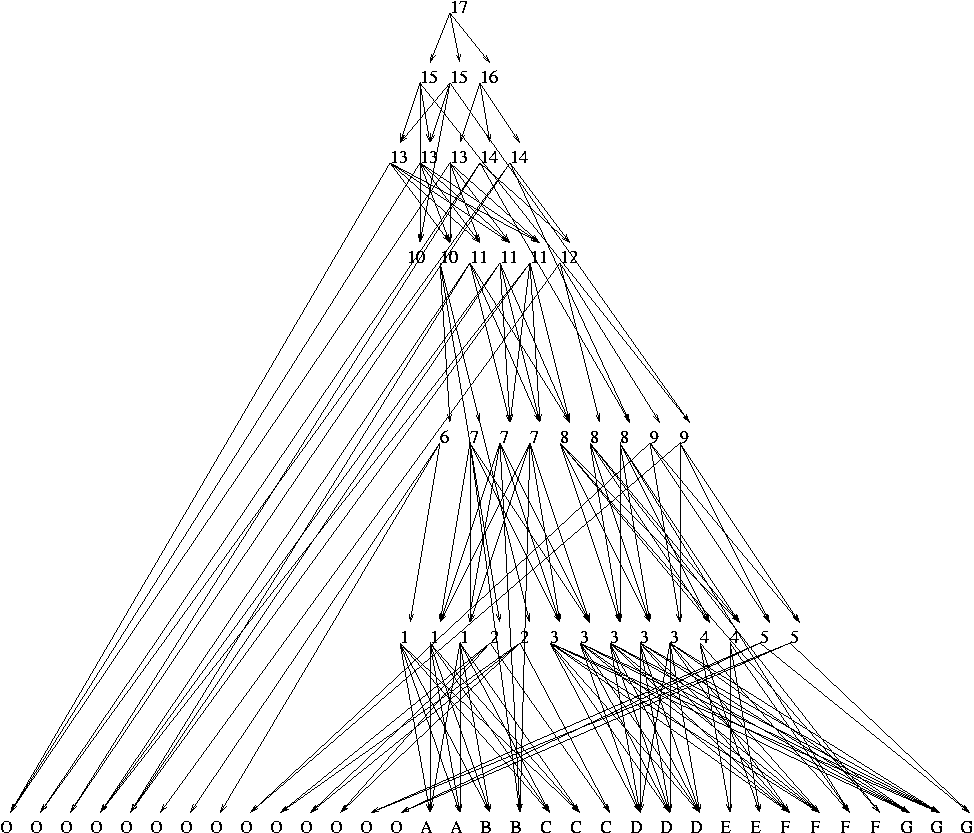
Now we wish to use this newly created data structure to query the location of a point. The faces that we have at each node are in fact triangles. Therefore, checking whether a point is inside any face is easy. We start the lookup at the root of the DAG. If the root triangle does not contain our point, clearly the point is outside our subdivision. Otherwise we check each of the nodes parents and recurse on the one that contains the point. Note that no two children of the same node can contain the same point because faces at the same level are never overlaping. Also, there may be at most 8 children for every node, because of the vertex degree limit that we imposed when constructing the structure. When we reach the last level, we return the label of the corresponding node.
Here's an example for a point lying inside original face F:
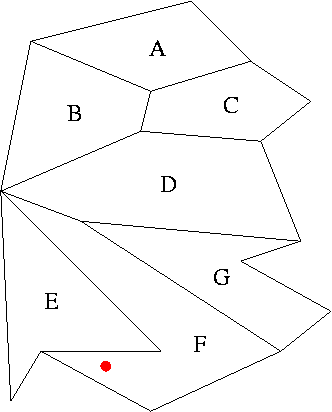
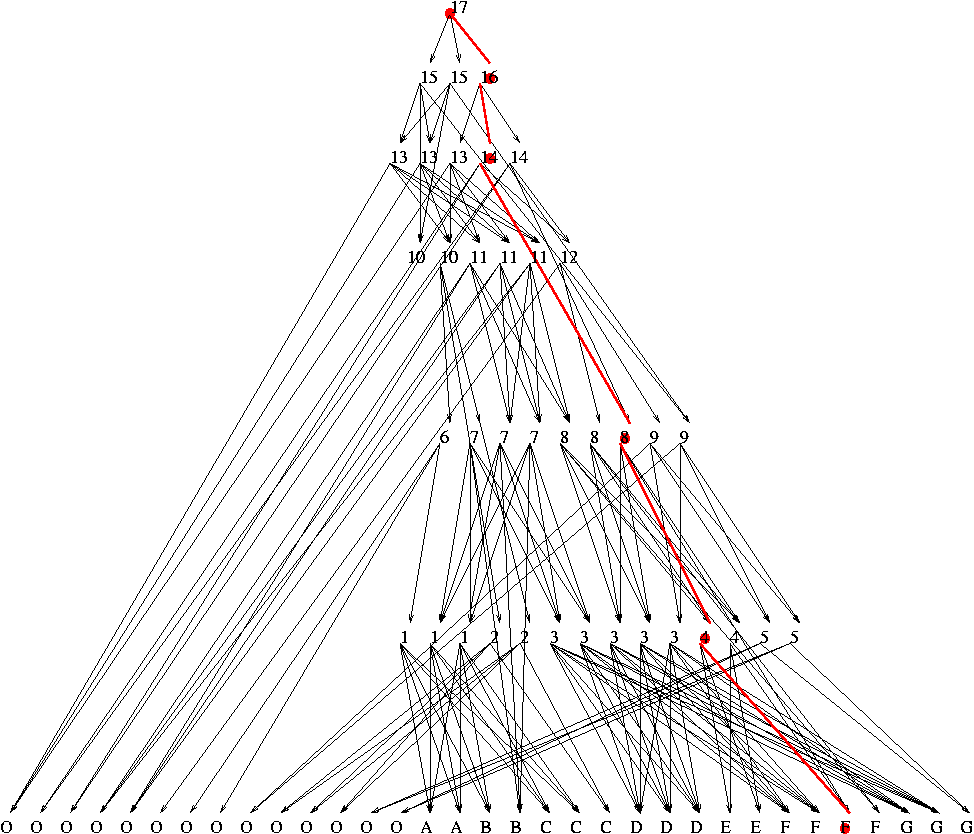
| Previous | Demonstration | About | Next |