Planar Point Location
Kirkpatrick's Point Location Data Structure
Problem:
We would like to be able to efficiently find the location of a point in a planar subdivision of the plane. This
subdivision is made of simple polygons like below:
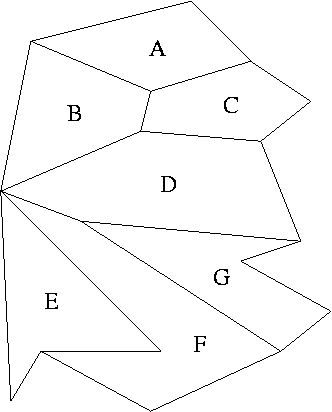
As you can see, every subdivision is identified by a label that we would like to return for each query point. For
this, we need to preprocess the subdivision into a data structure that allows fast searching.
Solution:
The one proposed by Kirkpatrick is able to answer a query in O(log n) time, where n is the number of
vertices in the subdivision. Kirkpatrick's data structure is a directed acyclic graph (DAG) having at every level a
different subdivision of the plane, with faces as nodes. The data structure assumes that the initial subdivision contains only triangles.
Therefore, if this is not true, the first thing to do is to triangulate it:
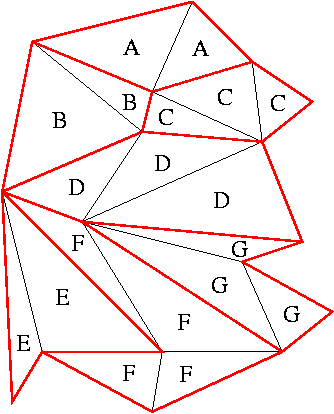
As you can see, triangles inherit labels from the face they belong to. Now, this is the actual subdivision that we
will be feeding to the algorithm that will construct the Kirkpatrick data structure. This probably gives a hint on how
the DAG produced will help us find the location of a point inside the original subdivision. Of course, it is easy to
test whether a point is inside a triangle or not: in counter-clockwise order, you only need to check whether any two
adjacent vertices of the triangle and the query point constitute a left turn or not. Therefore we will check if a point
is inside an original face by checking all the triangles that belong to it in the triangulation.


